Leonardo Fibonacci , matematyk włoski, w swojej książce Liber abaci zajął się problemem dotyczącym rozmnażania się stada królików.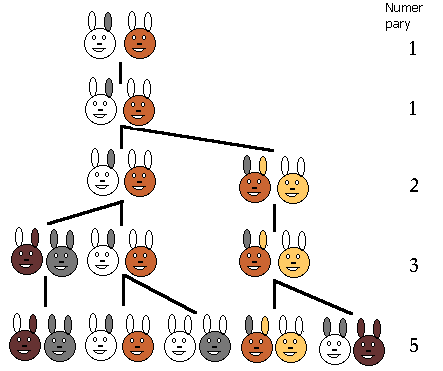
Zasady tego eksperymentu mentalnego są proste: zaczynamy od jednej pary, każda samica królika wydaje na świat potomstwo w miesiąc po kopulacji; konkretnie jednego samca i jedną samicę. W miesiąc po urodzeniu królik może przystąpić do reprodukcji.
Jak w takiej sytuacji będzie wyglądał rozwój naszej farmy, ile królików będzie liczyła po jednym roku? Przy końcu ostatniego miesiąca możemy się spodziewać krótkiego sparingu w pierwszej parze królików. Pod koniec drugiego miesiąca samica urodzi parę młodych tak więc na farmie będą już dwie pary. W trzecim miesiącu będziemy mieli już trzy pary, gdyż pierwsza samica wyda na świat kolejne potomstwo, a urodzone wcześniej przystąpi do kopulacji itd. W łatwy sposób można obliczyć, że liczebności w kolejnych miesiącach będą wynosić 1,1,2,3,5,8,13,21,34...
Kolejne jego elementy stanowią sumę dwóch wcześniejszych np. 21=13+8.
Szereg liczb obrazujący m.in. rozród królików nosi nazwę Ciągu Fibonacciego.
Stosunek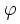 ma ścisły związek z ciągiem Fibonacciego. Stosunek dwóch kolenych liczb wyrazów w ciągu w miarę wzrastania jest coraz bliższy wartości 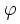.