






|
Spotkanie n osób
Ogólnie, gdy n osób X1, X2, X3, ... Xn umawia się na
spotkanie między chwilą 0 a 1 i każda deklaruje czas oczekiwania na pozostałych wynoszący ai,
to szanse na ich spotkanie możemy określić wyznaczając stosunek objętości n-wymiarowego zbioru
R(a1, a2, a3, ... , an) opisanego za pomocą nierówności
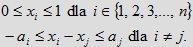 Mamy n nierówności typu 0 ≤ xi ≤ 1, natomiast nierówności typu
Mamy n nierówności typu 0 ≤ xi ≤ 1, natomiast nierówności typu
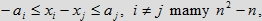 ale nierówności
ale nierówności
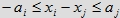 oraz
oraz
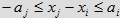 podają ten sam warunek, stąd różnych nierówności tego typu mamy
podają ten sam warunek, stąd różnych nierówności tego typu mamy 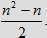 W przypadku najprostszym, gdy każda osoba deklaruje, że poczeka taką samą ilość czasu równą
W przypadku najprostszym, gdy każda osoba deklaruje, że poczeka taką samą ilość czasu równą
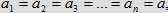 mamy zbiór R(a, a, a, ... , a) opisany przez nierówności
mamy zbiór R(a, a, a, ... , a) opisany przez nierówności
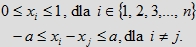 Zbiór ten jest sumą n-wymiarowej kostki o krawędzi a opisanej przez nierówności:
Zbiór ten jest sumą n-wymiarowej kostki o krawędzi a opisanej przez nierówności:
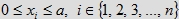 oraz n równoległościanów o wysokości 1−a i o podstawie, która jest (n−1)-wymiarową kostką
opisaną za pomocą nierówności:
oraz n równoległościanów o wysokości 1−a i o podstawie, która jest (n−1)-wymiarową kostką
opisaną za pomocą nierówności:
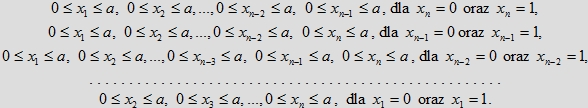 Każda z tych podstaw ma (n−1) wymiarową objętość równą an−1. Stąd objętość
każdego z tych równoległościanów wynosi (1−a)an−1. Wobec tego objętość zbioru
R(a, a, ... , a) w przypadku n osób wynosi
Każda z tych podstaw ma (n−1) wymiarową objętość równą an−1. Stąd objętość
każdego z tych równoległościanów wynosi (1−a)an−1. Wobec tego objętość zbioru
R(a, a, ... , a) w przypadku n osób wynosi
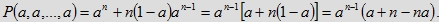 Zaobserwujmy, że jeśli każda z n osób deklaruje, że po przyjściu na wyznaczone miejsce spotkania poczeka 0,25
godziny (tzn. 0,25), to szanse na spotkanie wszystkich osób wynoszą odpowiednio dla n osób:
Zaobserwujmy, że jeśli każda z n osób deklaruje, że po przyjściu na wyznaczone miejsce spotkania poczeka 0,25
godziny (tzn. 0,25), to szanse na spotkanie wszystkich osób wynoszą odpowiednio dla n osób:
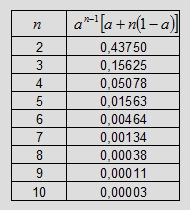 Tabela 8. Prawdopodobieństwo spotkania n osób, z których każda deklaruje, że poczeka na pozostałe 15 minut.
Wniosek. Szanse na doprowadzenie do spotkania sześciu lub większej liczby osób, z których każda ma przyjść
w ustalone miejsce spotkania między godziną dwunastą a trzynastą i po przyjściu poczekać na pozostałe osoby
kwadrans, jest mniejsze niż 1% (graniczy więc z cudem!)
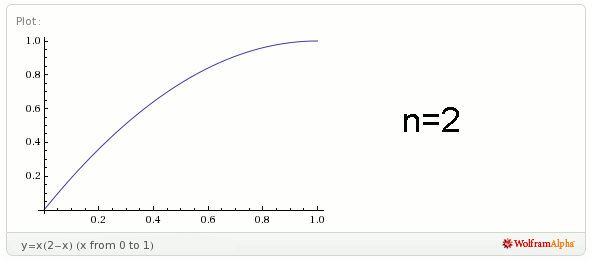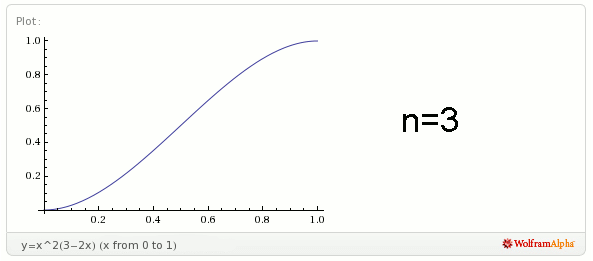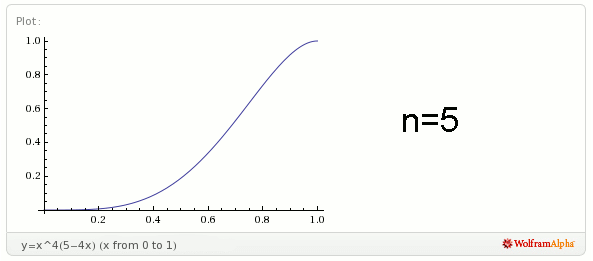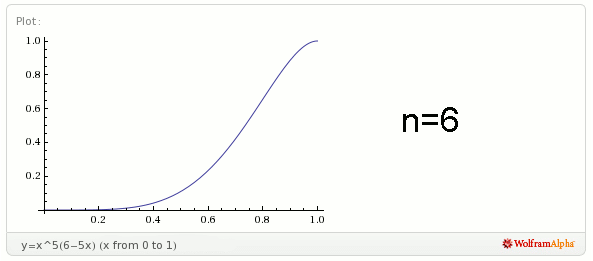
Spójrzmy na wykresy funkcji gdzie liczba osób − n, jest równe 2, 3, 4, 5, 6.
Zauważmy, że im więcej osób (im większe jest n), tym prawdopodobieństwo ich spotkania zaraz po godzinie dwunastej zmniejsza się.
Tabela 8. Prawdopodobieństwo spotkania n osób, z których każda deklaruje, że poczeka na pozostałe 15 minut.
Wniosek. Szanse na doprowadzenie do spotkania sześciu lub większej liczby osób, z których każda ma przyjść
w ustalone miejsce spotkania między godziną dwunastą a trzynastą i po przyjściu poczekać na pozostałe osoby
kwadrans, jest mniejsze niż 1% (graniczy więc z cudem!)
Spójrzmy na wykresy funkcji gdzie liczba osób − n, jest równe 2, 3, 4, 5, 6.
Zauważmy, że im więcej osób (im większe jest n), tym prawdopodobieństwo ich spotkania zaraz po godzinie dwunastej zmniejsza się.
|

