Autorzy wielu podręczników i zbiorów zadań z rachunku prawdopodobieństwa proponują rozwiązać następujący problem, zwany zadaniem o spotkaniu (meeting problem): W określonym miejscu między godziną dwunastą a trzynastą umawiają się na spotkanie dwie osoby i czekają jedna na drugą pewną liczbę minut, np. 15 lub 20. Jakie są szanse, że spotkają się? 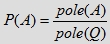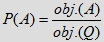Zwykle problem ten rozwiązuje się za pomocą pojęcia prawdopodobieństwa geometrycznego zajścia zdarzenia A w zbiorze Q: rozumianego jako iloraz pola zbioru A i pola zbioru Q w przypadku figur płaskich A ⊂ Q, które mają pole, a w przypadku brył A ⊂ Q, które mają objętość: jako iloraz ich objętości. Zadanie o spotkaniu jest prezentowane na wielu stronach internetowych poświęconych matematyce rekreacyjnej. Niektóre z nich proponują rozwiązania za pomocą rachunku całkowego. W pracy pokażemy, że można uzyskać ciekawe wnioski, prowadząc rozważania, w których posługiwać będziemy się prostymi modelami (w tym także modelami wykonanymi z klocków magnetycznych) i obliczeniami, wymagającymi znajomości wzoru na pole równoległoboku (w przypadku płaskim): 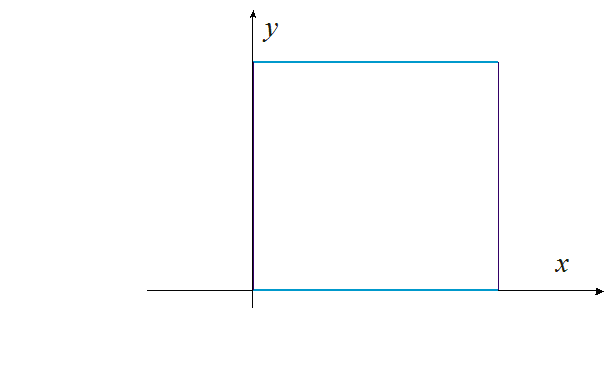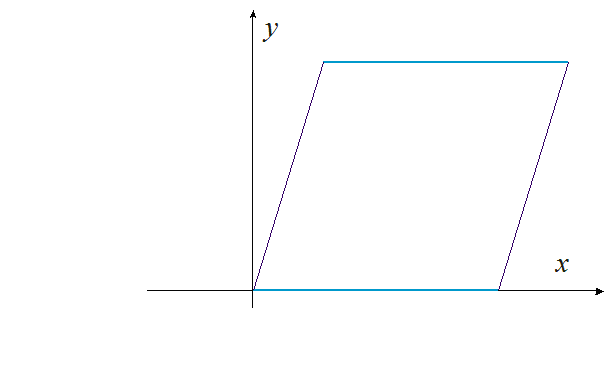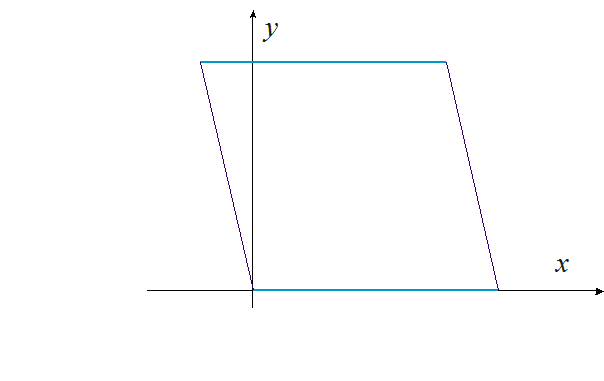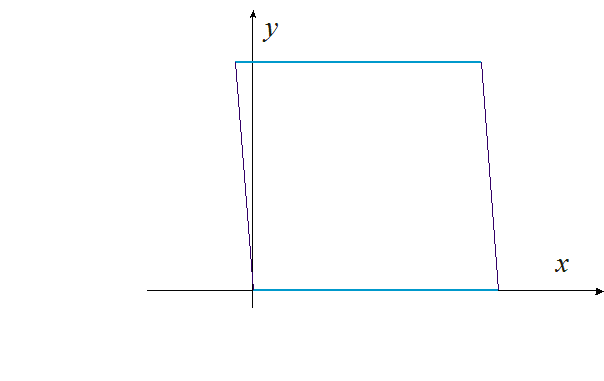Animacja 1. Pole równoległoboku równe jest iloczynowi jego podstawy i wysokości. Równoległoboki o równych podstawach i wysokościach mają równe pola. 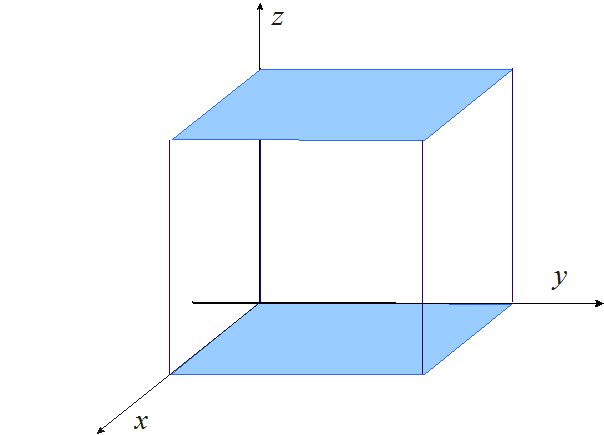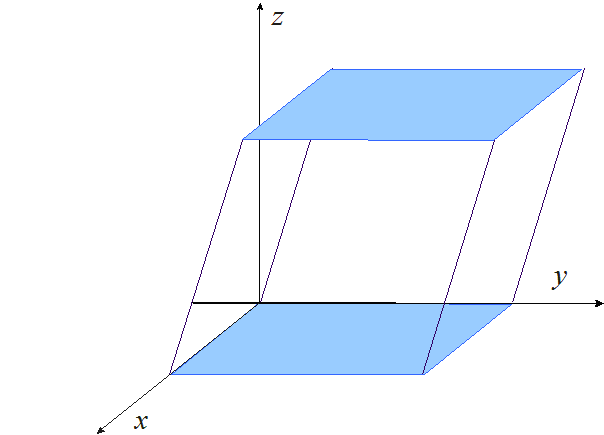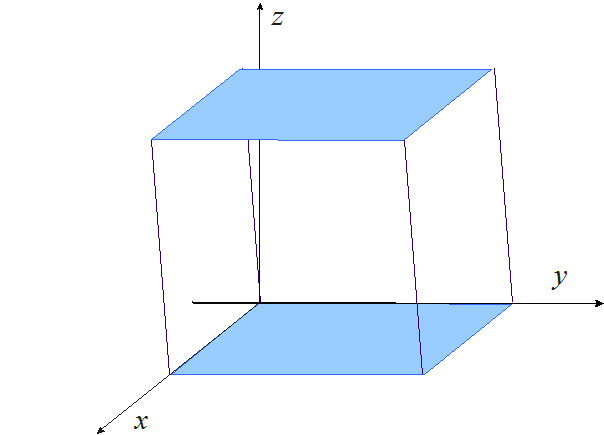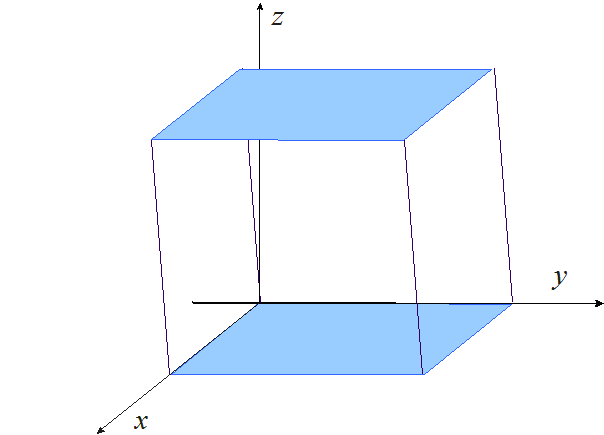i wzoru na objętość równoległościanu (w przypadku przestrzennym): Animacja 2. Objętość równoległościanu równa jest iloczynowi pola jego podstawy i wysokości. Równoległościany o równych podstawach i wysokościach mają równe objętości. Zaproponujemy rozwiązania, które będą prowadziły do prawdopodobieństwa geometrycznego, a także takie, które z niego bezpośrednio nie korzystają. Rozwiążemy także problem dla trzech i większej liczby osób, które umawiają się na spotkanie. Obliczymy jak długo powinny czekać osoby, które już przyszły, na przyjście pozostałych osób, aby szanse na spotkanie wyniosły 50%, 60%, 70%, 80% lub 90%. Wykorzystamy w tym celu arkusz kalkulacyjny. Zauważymy, że im większa grupa osób umawia się na spotkanie, tym mniejsze są szanse, że spotkanie dojdzie do skutku. Znamy ten fakt z własnego doświadczenia oraz np. z filmowych przygód Kevina, bohatera filmów Kevin sam w domu i Kevin w Nowym Jorku, który gubi się we własnym domu w dużej grupie krewnych w czasie gorączkowych przygotowań do wyjazdu na lotnisko.