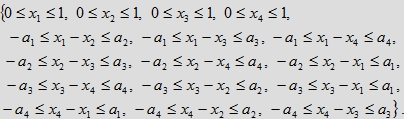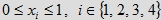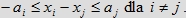Spotkanie czterech osób W przypadku czterech osób X1, X2, X3, X4 które deklarują, że będą czekać 60a1, 60a2, 60a3, 60a4 minut, za miarę prawdopodobieństwa ich spotkania możemy przyjąć stosunek czterowymiarowej objętości bryły R(a1, a2, a3, a4) opisanej za pomocą nierówności które krótko można zapisać następująco: oraz do czterowymiarowej objętości kostki 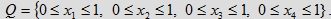Zarówno kostka Q jak i zbiór R(a1, a2, a3, a4) są równoległoœcianami, więc ich czterowymiarową objętość określimy podobnie jak w przypadku dwuwymiarowym i trójwymiarowym, mnożąc podstawę przez wysokość, a ściślej: mnożąc objętość trójwymiarowej podstawy przez wysokość. Rozważmy wpierw najprostszy przypadek, gdy wszystkie osoby deklarują taki sam czas oczekiwania, tzn. 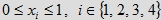a1 = a2 = a3 = a4 = a ∈ [0, 1], czyli zbiór R(a, a, a, a) opisują nierówności 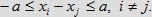Wówczas zbiór R(a, a, a, a) jest sumą czterowymiarowego zbioru 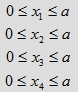o czterowymiarowej objętości równej a4 oraz czterech równoległościanów o wysokości 1−a, których podstawami są sześciany o objętości a3 opisane odpowiednio przez nierówności: 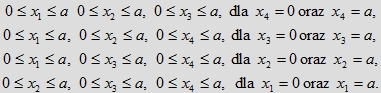Stąd czterowymiarowa objętość tej bryły wynosi 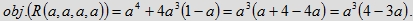Wobec tego stosunek objętości bryły R(a, a, a, a) do objętości kostki Q, który przyjmujemy za miarę prawdopodobieństwa spotkania czterech osób deklarujących taki sam czas oczekiwania na pozostałe, równy 60a minut, wyraża funkcja 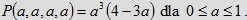Zauważmy, że dla 0 ≤ a ≤ 1 mamy: 0 ≤ P(a, a, a, a) ≤1. Naszkicujmy wykres funkcji 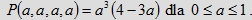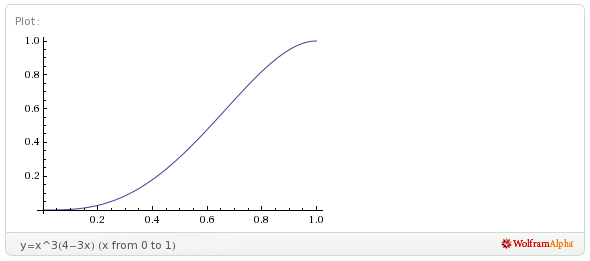W przypadku, gdy a=0,25 (tzn. każda osoba czeka kwadrans), szanse na spotkanie są niewielkie: 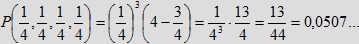Przypomnijmy, że w przypadku dwóch osób (w modelu IV) prawdopodobieństwo spotkania wynosi 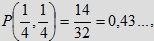a w przypadku trzech osób (w modelu A) otrzymaliśmy: 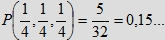co nas nie dziwi, gdyż pamiętamy, że spotkanie się w gronie czterech osób, z których każda ma przyjść w określonym czasie, jest trudne w realizacji.