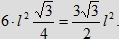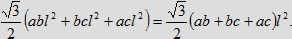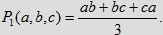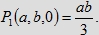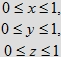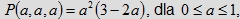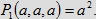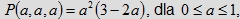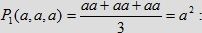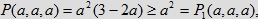Model A
Model B
Model A
Model B




|
Model B
Zamiast rozważać R(a, b, c) zrezygnujmy z nierówności:
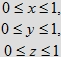 i rozważmy − podobnie jak w modelu VI w przypadku spotkania dwóch osób − zbiór:
i rozważmy − podobnie jak w modelu VI w przypadku spotkania dwóch osób − zbiór:
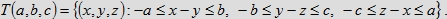 Zbiór ten poza sześcianem Q nie jest ograniczony. Ma jednak pewną zaletę: ma taki sam przekrój dowolną
płaszczyzną prostopadłą do przekątnej sześcianu Q łączącej punkty (0, 0, 0) oraz (1, 1, 1) Figurę, która
jest tym przekrojem, najwygodniej rozważać po zrzutowaniu bryły T(a, b, c) oraz sześcianu Q na
płaszczyznę prostopadłą do przekątnej o końcach (0, 0, 0) oraz (1, 1, 1).
Zbiór ten poza sześcianem Q nie jest ograniczony. Ma jednak pewną zaletę: ma taki sam przekrój dowolną
płaszczyzną prostopadłą do przekątnej sześcianu Q łączącej punkty (0, 0, 0) oraz (1, 1, 1) Figurę, która
jest tym przekrojem, najwygodniej rozważać po zrzutowaniu bryły T(a, b, c) oraz sześcianu Q na
płaszczyznę prostopadłą do przekątnej o końcach (0, 0, 0) oraz (1, 1, 1).
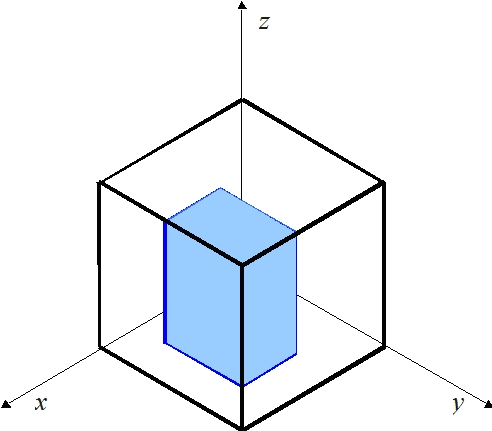 Rysunek 5. Rzut sześcianu Q oraz bryły T(a, b, c) na płaszczyznę prostopadłą do przekątnej
sześcianu Q przechodzącej przez punkty (0, 0, 0) oraz (1, 1, 1).
Zauważmy, że teraz za miarę prawdopodobieństwa spotkania trzech osób X, Y, Z możemy przyjąć stosunek pola
sześciokąta będącego rzutem bryły T(a, b, c) na rozważaną płaszczyznę do pola rzutu sześcianu Q na
tę płaszczyznę. Rzut ścian sześcianu jest sumą sześciu trójkątów równobocznych o polu:
Rysunek 5. Rzut sześcianu Q oraz bryły T(a, b, c) na płaszczyznę prostopadłą do przekątnej
sześcianu Q przechodzącej przez punkty (0, 0, 0) oraz (1, 1, 1).
Zauważmy, że teraz za miarę prawdopodobieństwa spotkania trzech osób X, Y, Z możemy przyjąć stosunek pola
sześciokąta będącego rzutem bryły T(a, b, c) na rozważaną płaszczyznę do pola rzutu sześcianu Q na
tę płaszczyznę. Rzut ścian sześcianu jest sumą sześciu trójkątów równobocznych o polu:
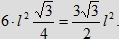 Natomiast rzut bryły T(a, b, c) jest sumą trzech równoległoboków o bokach odpowiednio al i bl, bl i cl, cl i al, których boki tworzą kąt 120 stopni. Stąd suma pól tych równoległoboków wynosi
Natomiast rzut bryły T(a, b, c) jest sumą trzech równoległoboków o bokach odpowiednio al i bl, bl i cl, cl i al, których boki tworzą kąt 120 stopni. Stąd suma pól tych równoległoboków wynosi
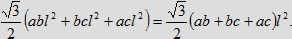 Wobec tego stosunek pól tych figur wynosi
Wobec tego stosunek pól tych figur wynosi
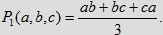 Uwaga. Jeśli a, b, c są liczbami z przedziału [0, 1], to P1(a, b, c) jest liczbą z
przedziału [0, 1].
Gdy dwie spośród liczb a, b, c są równe zeru, tzn. dwie osoby deklarują się, że po przyjściu ani chwili nie
będą czekać, to szanse na spotkanie się trzech osób są równe zeru:
Uwaga. Jeśli a, b, c są liczbami z przedziału [0, 1], to P1(a, b, c) jest liczbą z
przedziału [0, 1].
Gdy dwie spośród liczb a, b, c są równe zeru, tzn. dwie osoby deklarują się, że po przyjściu ani chwili nie
będą czekać, to szanse na spotkanie się trzech osób są równe zeru:
 Gdy jedna z osób deklaruje się, że nie będzie czekać (np. c=0), to
Gdy jedna z osób deklaruje się, że nie będzie czekać (np. c=0), to
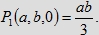 Wynika stąd, że nawet gdy pozostałe dwie osoby deklarują, że będą czekać po przyjściu pełną godzinę, szanse na
spotkanie się wszystkich trzech osób są nie większe niż jedna trzecia.
Uwaga. Przypomnijmy, że rezygnacja z nierówności
Wynika stąd, że nawet gdy pozostałe dwie osoby deklarują, że będą czekać po przyjściu pełną godzinę, szanse na
spotkanie się wszystkich trzech osób są nie większe niż jedna trzecia.
Uwaga. Przypomnijmy, że rezygnacja z nierówności
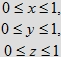 oznacza, że niekoniecznie zakładamy, że każda z trzech osób przyjdzie dopiero po godzinie 12 (być może przyjdzie
kilka minut wcześniej) i opuści wyznaczone miejsce spotkania najpóźniej o godzinie 13 (możliwe, że zaczeka kilka
minut po wybiciu pełnej godziny).
Porównajmy model A, w którym wyznaczyliśmy stosunek objętości bryły R(a, a, a) do objętości sześcianu Q
wyrażony przez funkcję
oznacza, że niekoniecznie zakładamy, że każda z trzech osób przyjdzie dopiero po godzinie 12 (być może przyjdzie
kilka minut wcześniej) i opuści wyznaczone miejsce spotkania najpóźniej o godzinie 13 (możliwe, że zaczeka kilka
minut po wybiciu pełnej godziny).
Porównajmy model A, w którym wyznaczyliśmy stosunek objętości bryły R(a, a, a) do objętości sześcianu Q
wyrażony przez funkcję
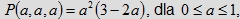 oraz model drugi, model B, w którym prawdopodobieństwo spotkania trzech osób mierzymy za pomocą stosunku pól
powierzchni rzutów bryły T(a, a, a) i sześcianu Q wyrażony przez
oraz model drugi, model B, w którym prawdopodobieństwo spotkania trzech osób mierzymy za pomocą stosunku pól
powierzchni rzutów bryły T(a, a, a) i sześcianu Q wyrażony przez
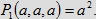 Narysujmy wykresy funkcji
Narysujmy wykresy funkcji 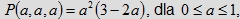
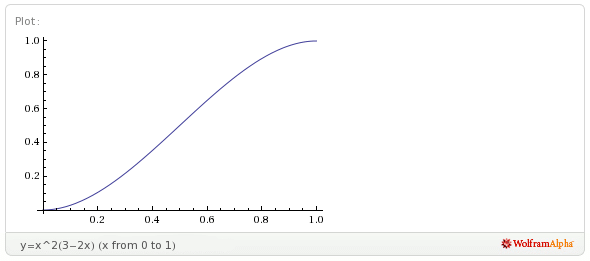 oraz funkcji
oraz funkcji 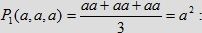
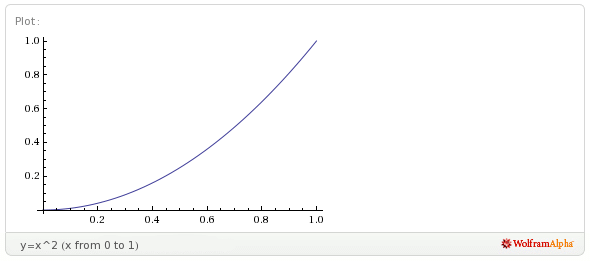 Zestawmy także wartości obu funkcji w tabeli:
Zestawmy także wartości obu funkcji w tabeli:
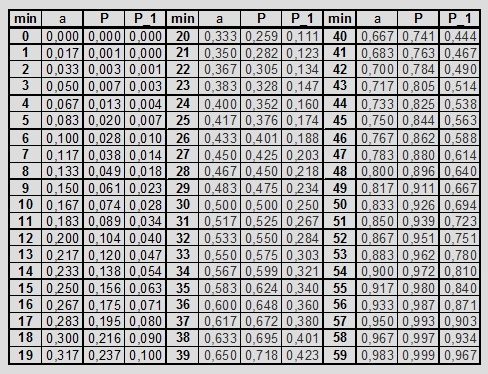 Tabela 7. Wartości prawdopodobieństwa spotkania trzech osób deklarujących taki sam czas oczekiwania w
modelu A, w którym za miarę prawdopodobieństwa przyjmujemy stosunek objętości brył R(a, a, a) i sześcianu Q
(kolumna P) oraz w modelu B, w którym za miarę prawdopodobieństwa spotkania przyjmujemy stosunek pól
powierzchni rzutu bryły T(a, a, a) do pola rzutu sześcianu Q (kolumna P_1).
Uwaga. Zauważmy, że dla dowolnej liczby 0 ≤ a ≤ 1 zachodzi nierówność:
Tabela 7. Wartości prawdopodobieństwa spotkania trzech osób deklarujących taki sam czas oczekiwania w
modelu A, w którym za miarę prawdopodobieństwa przyjmujemy stosunek objętości brył R(a, a, a) i sześcianu Q
(kolumna P) oraz w modelu B, w którym za miarę prawdopodobieństwa spotkania przyjmujemy stosunek pól
powierzchni rzutu bryły T(a, a, a) do pola rzutu sześcianu Q (kolumna P_1).
Uwaga. Zauważmy, że dla dowolnej liczby 0 ≤ a ≤ 1 zachodzi nierówność:
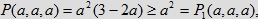 gdyż
gdyż
 Oznacza to, że prawdopodobieństwo spotkania w modelu B jest mniejsze niż w modelu A dla 0 ≤ a ≤ 1.
Prawdopodobieństwa te są równe tylko dla skrajnych wartości a=0 i a=1. Innymi słowy, przyjmując
prostszy rachunkowo model B, w którym zrezygnowaliśmy z wyznaczania objętości bryły R(a, b, b) z modelu A,
jesteśmy zmuszeni zadeklarować w modelu B dłuższy czas oczekiwania na przyjście pozostałych osób niż w modelu A,
aby z ustalonym prawdopodobieństwem doprowadzić do spotkania trzech osób.
Oznacza to, że prawdopodobieństwo spotkania w modelu B jest mniejsze niż w modelu A dla 0 ≤ a ≤ 1.
Prawdopodobieństwa te są równe tylko dla skrajnych wartości a=0 i a=1. Innymi słowy, przyjmując
prostszy rachunkowo model B, w którym zrezygnowaliśmy z wyznaczania objętości bryły R(a, b, b) z modelu A,
jesteśmy zmuszeni zadeklarować w modelu B dłuższy czas oczekiwania na przyjście pozostałych osób niż w modelu A,
aby z ustalonym prawdopodobieństwem doprowadzić do spotkania trzech osób.
|




 Model A
Model B
Model A
Model B




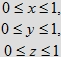
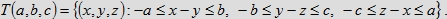
 Rysunek 5. Rzut sześcianu Q oraz bryły T(a, b, c) na płaszczyznę prostopadłą do przekątnej
sześcianu Q przechodzącej przez punkty (0, 0, 0) oraz (1, 1, 1).
Rysunek 5. Rzut sześcianu Q oraz bryły T(a, b, c) na płaszczyznę prostopadłą do przekątnej
sześcianu Q przechodzącej przez punkty (0, 0, 0) oraz (1, 1, 1).