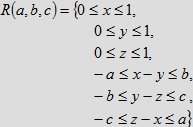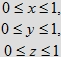Model A
Model B
Model A
Model B




|
Model A
Rozważmy szanse na spotkanie trzech osób X, Y i Z, które deklarują się, że przyjdą w ustalone miejsce między
godziną 12 a 13, i poczekają odpowiednio 60a, 60b, 60c minut. Zdarzenie, że wszystkie trzy osoby spotkają się, opisuje
zbiór
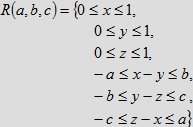 zawarty w sześcianie o krawędzi jednostkowej
zawarty w sześcianie o krawędzi jednostkowej
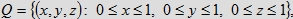 który reprezentuje wszystkie możliwe chwile przyjścia x, y, z osób X, Y, Z pomiędzy godziną 12 (którą będziemy określać
jako chwila 0), a godziną 13 (chwila 1).
Przypadek, w którym każda z trzech osób deklaruje taki sam czas oczekiwania.
Rozważmy najpierw przypadek, w którym każda z trzech osób czeka taką sama liczbę minut po przyjściu na miejsce
spotkania. Na początek narysujmy osobno wykresy zbiorów punktów (x, y, z) które przedstawiają sytuację spotkania par osób,
tj. osoby X z Y, które dojdzie do skutku, gdy chwile x oraz y przyjścia tych osób spełniają nierówność
−a ≤ x−y ≤ a,
a chwila przyjścia osoby trzeciej Z jest dowolną liczbą z przedziału [0, 1]:
który reprezentuje wszystkie możliwe chwile przyjścia x, y, z osób X, Y, Z pomiędzy godziną 12 (którą będziemy określać
jako chwila 0), a godziną 13 (chwila 1).
Przypadek, w którym każda z trzech osób deklaruje taki sam czas oczekiwania.
Rozważmy najpierw przypadek, w którym każda z trzech osób czeka taką sama liczbę minut po przyjściu na miejsce
spotkania. Na początek narysujmy osobno wykresy zbiorów punktów (x, y, z) które przedstawiają sytuację spotkania par osób,
tj. osoby X z Y, które dojdzie do skutku, gdy chwile x oraz y przyjścia tych osób spełniają nierówność
−a ≤ x−y ≤ a,
a chwila przyjścia osoby trzeciej Z jest dowolną liczbą z przedziału [0, 1]:
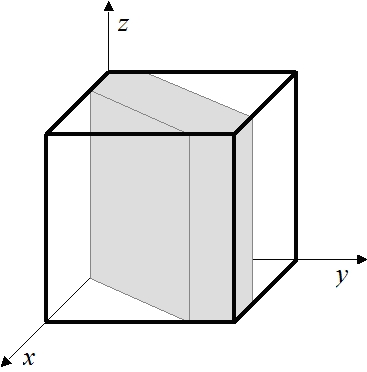 Fakt spotkania osób Y i Z opisuje nierówność:
−a ≤ y−z ≤ a
przy czym x jest dowolną liczbą z przedziału [0, 1]:
Fakt spotkania osób Y i Z opisuje nierówność:
−a ≤ y−z ≤ a
przy czym x jest dowolną liczbą z przedziału [0, 1]:
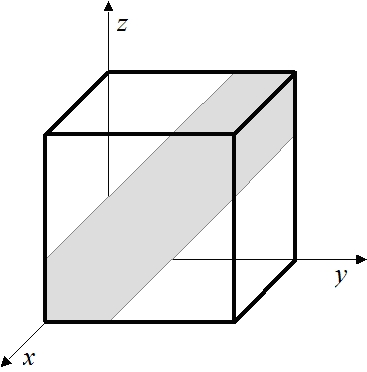 Natomiast spotkanie osób X i Z opisuje nierówność:
−a ≤ x−z ≤ a
przy czym y jest dowolną liczbą z przedziału [0, 1]:
Natomiast spotkanie osób X i Z opisuje nierówność:
−a ≤ x−z ≤ a
przy czym y jest dowolną liczbą z przedziału [0, 1]:
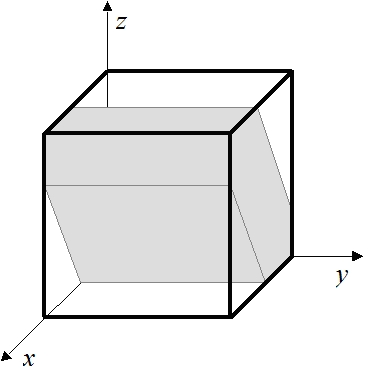 Zauważmy, że częścią wspólną trzech graniastosłupów jest bryła, która składa się z sześcianu o boku a i trzech
graniastosłupów pochyłych, w których podstawie znajduje się kwadrat o boku a i mających wysokość równą 1−a.
Zbiór R(a, a, a) ma objętość równą
Zauważmy, że częścią wspólną trzech graniastosłupów jest bryła, która składa się z sześcianu o boku a i trzech
graniastosłupów pochyłych, w których podstawie znajduje się kwadrat o boku a i mających wysokość równą 1−a.
Zbiór R(a, a, a) ma objętość równą
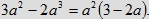
 Rysunek 4. Sześcian Q oraz zbiór R(a, a, a) w modelu A.
Przedstawmy także model zbioru wykonany z klocków magnetycznych (animacja 6):
Rysunek 4. Sześcian Q oraz zbiór R(a, a, a) w modelu A.
Przedstawmy także model zbioru wykonany z klocków magnetycznych (animacja 6):
 Przyjmijmy stosunek objętości bryły R(a, a, a) do objętości sześcianu Q za miarę szansy spotkania się
osób X, Y, Z. Mamy więc
Przyjmijmy stosunek objętości bryły R(a, a, a) do objętości sześcianu Q za miarę szansy spotkania się
osób X, Y, Z. Mamy więc
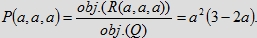 Uwaga. Funkcja
Uwaga. Funkcja
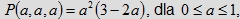 przyjmuje dla a∈[0, 1] wartoci w przedziale od 0 do 1.
Uwaga. Gdy a=0, to P(0, 0, 0)=0, co nas nie dziwi, gdyż nie ma szans na spotkanie trzech osób
przychodzących o różnych porach x, y, z, gdy żadna z nich nie poczeka na pozostałe ani chwili.
Gdy a=0,25 (tzn. osoby X, Y i Z deklarują, że poczekają kwadrans po przyjściu na pozostałe osoby), to
przyjmuje dla a∈[0, 1] wartoci w przedziale od 0 do 1.
Uwaga. Gdy a=0, to P(0, 0, 0)=0, co nas nie dziwi, gdyż nie ma szans na spotkanie trzech osób
przychodzących o różnych porach x, y, z, gdy żadna z nich nie poczeka na pozostałe ani chwili.
Gdy a=0,25 (tzn. osoby X, Y i Z deklarują, że poczekają kwadrans po przyjściu na pozostałe osoby), to
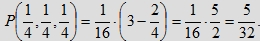 Porównajmy to prawdopodobieństwo z prawdopodobieństwem spotkania dwóch osób w modelu czwartym:
Porównajmy to prawdopodobieństwo z prawdopodobieństwem spotkania dwóch osób w modelu czwartym:
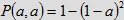 co w przypadku, gdy a=0,25, daje
co w przypadku, gdy a=0,25, daje
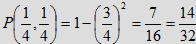 czyli więcej niż w przypadku trzech osób. Nie powinno to nas dziwić, gdyż umówienie się trzech osób na spotkanie
jest bardziej kłopotliwe niż dwóch.
Porównajmy wykresy prawdopodobieństw spotkania się dwóch osób w modelu IV
(prawdopodobieństwo to wyraża funkcja
czyli więcej niż w przypadku trzech osób. Nie powinno to nas dziwić, gdyż umówienie się trzech osób na spotkanie
jest bardziej kłopotliwe niż dwóch.
Porównajmy wykresy prawdopodobieństw spotkania się dwóch osób w modelu IV
(prawdopodobieństwo to wyraża funkcja 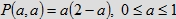 : :
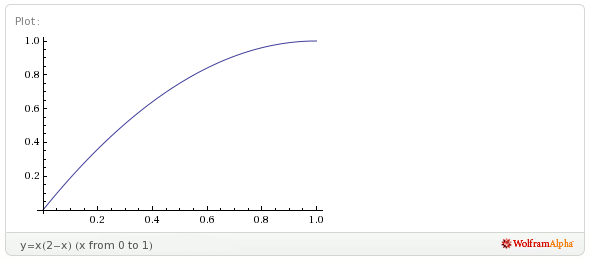 oraz w przypadku trzech osób w modelu A
(prawdopodobieństwo to wyraża funkcja
oraz w przypadku trzech osób w modelu A
(prawdopodobieństwo to wyraża funkcja 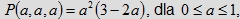 : :
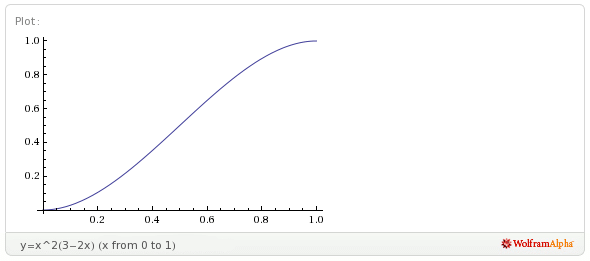 gdy każda z nich deklaruje, że poczeka minut po przyjściu.
Podajmy także w tabeli, wartości funkcji
gdy każda z nich deklaruje, że poczeka minut po przyjściu.
Podajmy także w tabeli, wartości funkcji 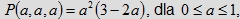 : :
 Tabela 5. Wartości prawdopodobieństwa (kolumna P) spotkania trzech osób, z których każda czeka na
pozostałe dwie osoby nie dłużej niż przez 60a minut (kolumna min) po przyjściu na miejsce spotkania.
Korzystając z danych, które zawarliśmy w tabelach 3 i 5, wyznaczmy, ile czasu powinna poczekać każda z trzech osób
na dwie pozostałe, aby szanse na spotkanie wynosiły co najmniej: 50%, 60%, 70%, 80%, 90%:
Tabela 5. Wartości prawdopodobieństwa (kolumna P) spotkania trzech osób, z których każda czeka na
pozostałe dwie osoby nie dłużej niż przez 60a minut (kolumna min) po przyjściu na miejsce spotkania.
Korzystając z danych, które zawarliśmy w tabelach 3 i 5, wyznaczmy, ile czasu powinna poczekać każda z trzech osób
na dwie pozostałe, aby szanse na spotkanie wynosiły co najmniej: 50%, 60%, 70%, 80%, 90%:
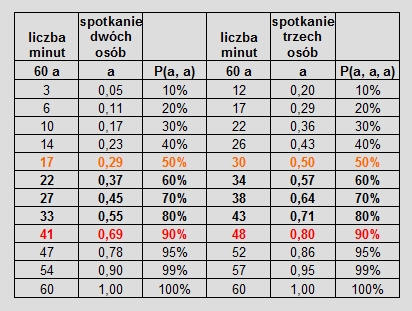 Tabela 6. Długość czasu oczekiwania na przyjście pozostałych osób (w kolumnie liczba minut) niezbędna do
osiągnięcia prawdopodobieństwa spotkania z prawdopodobieństwem P(a, a) w przypadku grupy dwuosobowej oraz z
prawdopodobieństwem P(a, a, a) w przypadku grupy złożonej z trzech osób.
Przypadek, w którym każda z trzech osób deklaruje różny czas oczekiwania.
Przypadek trzech osób X, Y, Z i dowolnych okresów a, b, c czasu oczekiwania na przyjście pozostałych
osób sprowadza się do wyznaczenia objętości bryły
Tabela 6. Długość czasu oczekiwania na przyjście pozostałych osób (w kolumnie liczba minut) niezbędna do
osiągnięcia prawdopodobieństwa spotkania z prawdopodobieństwem P(a, a) w przypadku grupy dwuosobowej oraz z
prawdopodobieństwem P(a, a, a) w przypadku grupy złożonej z trzech osób.
Przypadek, w którym każda z trzech osób deklaruje różny czas oczekiwania.
Przypadek trzech osób X, Y, Z i dowolnych okresów a, b, c czasu oczekiwania na przyjście pozostałych
osób sprowadza się do wyznaczenia objętości bryły
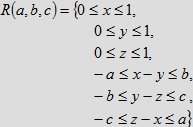 co nie jest łatwe.
Dlatego zrezygnujmy z nierówności:
co nie jest łatwe.
Dlatego zrezygnujmy z nierówności:
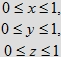 i rozwišżemy to jak w modelu VI w przypadku spotkania dwóch osób (patrz Model B).
i rozwišżemy to jak w modelu VI w przypadku spotkania dwóch osób (patrz Model B).
|




 Model A
Model B
Model A
Model B




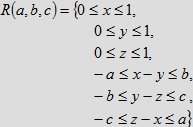
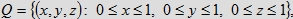



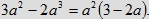
 Rysunek 4. Sześcian Q oraz zbiór R(a, a, a) w modelu A.
Rysunek 4. Sześcian Q oraz zbiór R(a, a, a) w modelu A.
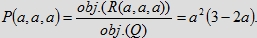
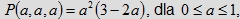
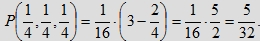
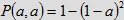
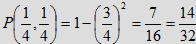
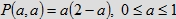 :
:

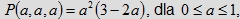 :
:

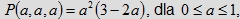 :
: