
 Model I
Model II
Model III
Model IV
Model V
Model VI
Model I
Model II
Model III
Model IV
Model V
Model VI





|
Model VI
Gdy liczby a i b, tj. okresy czasu oczekiwania deklarowane przez obie osoby X oraz Y
są małymi liczbami, to pole P(a, b) figury R(a, b) figury mało różni się od sumy pól dwóch
równoległoboków o podstawach odpowiednio a oraz b i równych wysokościach o długości 1. Stąd zamiast
brać stosunek pól − pola figury R(a, b) do pola kwadratu Q można rozważyć szerokość pasa:
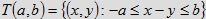 do długości przekątnej S kwadratu Q, która łączy punkty (1,0) i (0,1).
Wtedy miarą prawdopodobieństwa spotkania X z Y jest stosunek:
do długości przekątnej S kwadratu Q, która łączy punkty (1,0) i (0,1).
Wtedy miarą prawdopodobieństwa spotkania X z Y jest stosunek:
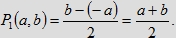
 Rysunek 3. Zbiory T(a, b) oraz R(a, b) w modelu VI.
Model ten opisuje sytuację spotkania dwóch osób bez żądania, że X i przyjdą dopiero po godzinie
dwunastej i obowiązkowo opuszczą miejsce spotkania o godzinie 13.
Uwaga. Jeśli a=1 (tzn. X czeka po przyjściu do końca pełnej godziny), a b=0 (tzn.
Y przychodzi i, jeśli nie spotka X, odchodzi od razu), to − podobnie jak w modelu piątym −
mamy
Rysunek 3. Zbiory T(a, b) oraz R(a, b) w modelu VI.
Model ten opisuje sytuację spotkania dwóch osób bez żądania, że X i przyjdą dopiero po godzinie
dwunastej i obowiązkowo opuszczą miejsce spotkania o godzinie 13.
Uwaga. Jeśli a=1 (tzn. X czeka po przyjściu do końca pełnej godziny), a b=0 (tzn.
Y przychodzi i, jeśli nie spotka X, odchodzi od razu), to − podobnie jak w modelu piątym −
mamy
 Czy to możliwe? Tak, bo osoba X, mimo że czeka pełną godzinę, może przyjść w dowolnej chwili między
chwilą 0 a 1 (czyli między godziną 12 a 13), czyli w szczególności po tym momencie y, w którym osoba
Y przyszła i odeszła.
Natomiast jeśli a=0 i b=0 to − również jak w modelu piątym − mamy
P1(a, b)=0 co zgadza się z rzeczywistością, bo jeśli X przyjdzie w chwili x i
pójdzie sobie, nie czekając ani chwili na drugą osobę, a Y podobnie przyjdzie w chwili y i również
sobie zaraz pójdzie, nie czekając na X, a x≠y, to nie ma szans, aby osoby te spotkały się.
Gdy zaś a=1 i b=1, to nie ma znaczenia, kiedy przyjdą X oraz Y − byle przyszli w
pewnym momencie x oraz y między chwilą 0 a 1. Gdy będą czekać pełne godziny po przyjściu, to prędzej,
czy później X doczeka się przyjścia Y albo Y doczeka się X, stąd P1(1, 1)=1.
Czy to możliwe? Tak, bo osoba X, mimo że czeka pełną godzinę, może przyjść w dowolnej chwili między
chwilą 0 a 1 (czyli między godziną 12 a 13), czyli w szczególności po tym momencie y, w którym osoba
Y przyszła i odeszła.
Natomiast jeśli a=0 i b=0 to − również jak w modelu piątym − mamy
P1(a, b)=0 co zgadza się z rzeczywistością, bo jeśli X przyjdzie w chwili x i
pójdzie sobie, nie czekając ani chwili na drugą osobę, a Y podobnie przyjdzie w chwili y i również
sobie zaraz pójdzie, nie czekając na X, a x≠y, to nie ma szans, aby osoby te spotkały się.
Gdy zaś a=1 i b=1, to nie ma znaczenia, kiedy przyjdą X oraz Y − byle przyszli w
pewnym momencie x oraz y między chwilą 0 a 1. Gdy będą czekać pełne godziny po przyjściu, to prędzej,
czy później X doczeka się przyjścia Y albo Y doczeka się X, stąd P1(1, 1)=1.
|



 Model I
Model II
Model III
Model IV
Model V
Model VI
Model I
Model II
Model III
Model IV
Model V
Model VI





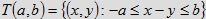
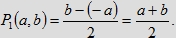
 Rysunek 3. Zbiory T(a, b) oraz R(a, b) w modelu VI.
Rysunek 3. Zbiory T(a, b) oraz R(a, b) w modelu VI.
