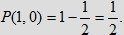Model I
Model II
Model III
Model IV
Model V
Model VI
Model I
Model II
Model III
Model IV
Model V
Model VI





|
Model V
Zastanówmy się jak będzie wyglądała sytuacja, w przypadku, gdy pierwsza osoba X będzie czekać 60a minut, a
druga osoba Y inną liczbę minut, powiedzmy 60b minut.
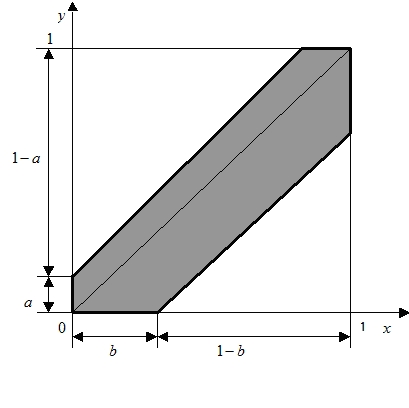 Rysunek 2. Zbiory Q oraz R(a, b) w modelu V.
W tym przypadku szanse spotkania osób X i Y pomiędzy godziną dwunastą a trzynastą opisuje stosunek
pola figury
Rysunek 2. Zbiory Q oraz R(a, b) w modelu V.
W tym przypadku szanse spotkania osób X i Y pomiędzy godziną dwunastą a trzynastą opisuje stosunek
pola figury
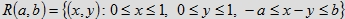 do pola kwadratu
do pola kwadratu 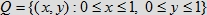 o boku jednostkowym.
Pole figury R(a, b) policzymy odejmując od pola kwadratu jednostkowego Q pola dwóch trójkątów równoramiennych o
ramionach długości 1−a i 1−b, stąd otrzymujemy prawdopodobieństwo spotkania osób X i Y
wyrażone za pomocą wzoru o boku jednostkowym.
Pole figury R(a, b) policzymy odejmując od pola kwadratu jednostkowego Q pola dwóch trójkątów równoramiennych o
ramionach długości 1−a i 1−b, stąd otrzymujemy prawdopodobieństwo spotkania osób X i Y
wyrażone za pomocą wzoru
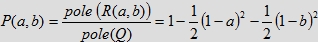 .
Uwaga. Jeśli a=1 (tzn. X czeka po przyjściu do końca pełnej godziny), a b=0 (tzn. Y
przychodzi i, jeśli nie spotka X, odchodzi od razu), to .
Uwaga. Jeśli a=1 (tzn. X czeka po przyjściu do końca pełnej godziny), a b=0 (tzn. Y
przychodzi i, jeśli nie spotka X, odchodzi od razu), to
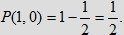 Czy to możliwe? Tak, bo osoba X, mimo że czeka pełną godzinę (ale nie dłużej niż do godziny pierwszej,
czyli ściślej: do końca pełnej godziny) może przyjść w dowolnej chwili między chwilą 0 a 1 (czyli między godziną 12
a 13), czyli w szczególności po tym momencie y, w którym osoba Y przyszła i odeszła.
Natomiast jeśli a=0 i b=0, to P(a, b)=0, co zgadza się z rzeczywistością, bo jeśli X przyjdzie
w chwili x i pójdzie sobie, nie czekając ani chwili na drugą osobę, a Y podobnie przyjdzie w chwili
y i również sobie zaraz pójdzie, nie czekając na X, a x≠y, to nie ma szans, aby się spotkali.
Gdy zaś a=1 i b, to niezależnie kiedy przyjdą X oraz Y, gdy będą czekać pełne godziny
po przyjściu (ale nie dłużej niż do godziny pierwszej), to prędzej, czy później X doczeka się przyjścia
Y albo Y doczeka się X, stąd P(1, 1)=1.
Czy to możliwe? Tak, bo osoba X, mimo że czeka pełną godzinę (ale nie dłużej niż do godziny pierwszej,
czyli ściślej: do końca pełnej godziny) może przyjść w dowolnej chwili między chwilą 0 a 1 (czyli między godziną 12
a 13), czyli w szczególności po tym momencie y, w którym osoba Y przyszła i odeszła.
Natomiast jeśli a=0 i b=0, to P(a, b)=0, co zgadza się z rzeczywistością, bo jeśli X przyjdzie
w chwili x i pójdzie sobie, nie czekając ani chwili na drugą osobę, a Y podobnie przyjdzie w chwili
y i również sobie zaraz pójdzie, nie czekając na X, a x≠y, to nie ma szans, aby się spotkali.
Gdy zaś a=1 i b, to niezależnie kiedy przyjdą X oraz Y, gdy będą czekać pełne godziny
po przyjściu (ale nie dłużej niż do godziny pierwszej), to prędzej, czy później X doczeka się przyjścia
Y albo Y doczeka się X, stąd P(1, 1)=1.
|



 Model I
Model II
Model III
Model IV
Model V
Model VI
Model I
Model II
Model III
Model IV
Model V
Model VI





 Rysunek 2. Zbiory Q oraz R(a, b) w modelu V.
Rysunek 2. Zbiory Q oraz R(a, b) w modelu V.
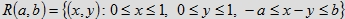
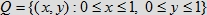 o boku jednostkowym.
Pole figury R(a, b) policzymy odejmując od pola kwadratu jednostkowego Q pola dwóch trójkątów równoramiennych o
ramionach długości 1−a i 1−b, stąd otrzymujemy prawdopodobieństwo spotkania osób X i Y
wyrażone za pomocą wzoru
o boku jednostkowym.
Pole figury R(a, b) policzymy odejmując od pola kwadratu jednostkowego Q pola dwóch trójkątów równoramiennych o
ramionach długości 1−a i 1−b, stąd otrzymujemy prawdopodobieństwo spotkania osób X i Y
wyrażone za pomocą wzoru
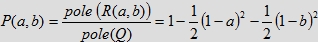 .
.