Model I
Model II
Model III
Model IV
Model V
Model VI
Model I
Model II
Model III
Model IV
Model V
Model VI





|
Model IV
Rozważmy także przypadek, w którym obie osoby mierzą czas z dokładnością tak wielką, jak tylko jest to możliwe,
np. z dokładnością co do sekundy lub większą:
 Niech
Niech
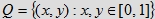 będzie zbiorem par liczb oraz oznaczających chwile przyjścia pierwszej i drugiej osoby.
Niech
będzie zbiorem par liczb oraz oznaczających chwile przyjścia pierwszej i drugiej osoby.
Niech
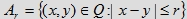 , gdzie , gdzie 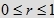 będzie zbiorem tych chwil przyjścia pierwszej i drugiej osoby, pomiędzy którymi różnica nie przekracza ustalonej
z góry przez obie osoby wartości czasu r, po upływie którego osoby odchodzą z miejsca spotkania, jeśli nie
doczekają się drugiej osoby.
Przyjmijmy za miarę prawdopodobieństwa zdarzenia Ar prawdopodobieństwo geometryczne tego zbioru
w zbiorze
będzie zbiorem tych chwil przyjścia pierwszej i drugiej osoby, pomiędzy którymi różnica nie przekracza ustalonej
z góry przez obie osoby wartości czasu r, po upływie którego osoby odchodzą z miejsca spotkania, jeśli nie
doczekają się drugiej osoby.
Przyjmijmy za miarę prawdopodobieństwa zdarzenia Ar prawdopodobieństwo geometryczne tego zbioru
w zbiorze , czyli iloraz pól tych zbiorów:
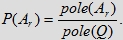
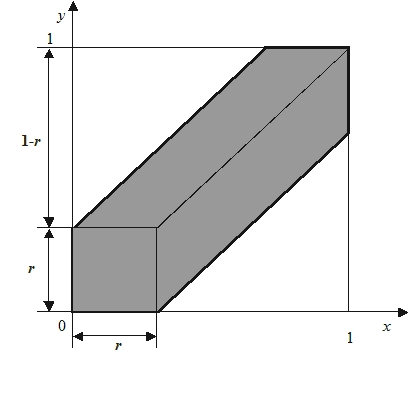 Rysunek 1. Zbiór Q i jego podzbiór Ar w modelu IV.
Zauważmy, że pole figury Ar możemy obliczyć, odejmując od pola kwadratu Q o boku
jednostkowym pola dwóch trójkątów prostokątnych równoramiennych o ramionach długości 1−r:
Rysunek 1. Zbiór Q i jego podzbiór Ar w modelu IV.
Zauważmy, że pole figury Ar możemy obliczyć, odejmując od pola kwadratu Q o boku
jednostkowym pola dwóch trójkątów prostokątnych równoramiennych o ramionach długości 1−r:
 lub − co prowadzi do tego samego wyniku − do pola kwadratu o boku r dodać pola dwóch
równoległoboków o podstawie r i wysokości 1−r.
Stąd prawdopodobieństwo zdarzenia Ar wyraża
lub − co prowadzi do tego samego wyniku − do pola kwadratu o boku r dodać pola dwóch
równoległoboków o podstawie r i wysokości 1−r.
Stąd prawdopodobieństwo zdarzenia Ar wyraża
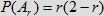 , gdzie , gdzie 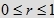 .
Narysujmy wykres funkcji: .
Narysujmy wykres funkcji:
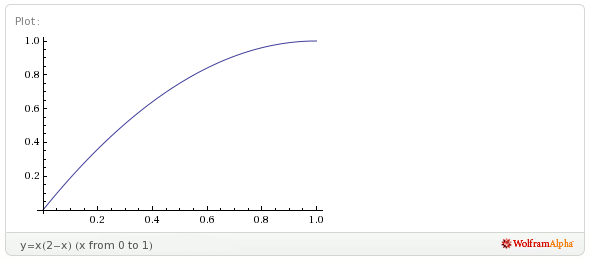 Podajmy wartości tej funkcji dla całkowitej liczby minut:
Podajmy wartości tej funkcji dla całkowitej liczby minut:
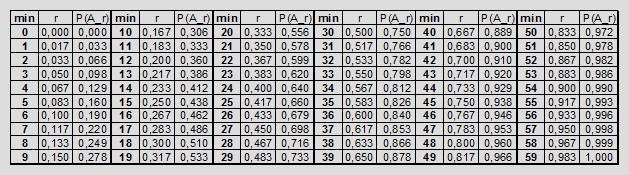 Tabela 4. Wartości prawdopodobieństwa spotkania w przypadku, gdy obie osoby zadeklarują czas oczekiwania równy
60r minut po przyjściu na miejsce spotkania w modelu IV.
Wniosek. Jeśli obie osoby odmierzają czas oczekiwania z bardzo dużą dokładnością, to spotkanie dojdzie do
skutku z prawdopodobieństwem 50%, jeśli obie osoby zadeklarują, że poczekają co najmniej osiemnaście minut po
przyjściu. Natomiast prawdopodobieństwo to wzrośnie do 90% dopiero wtedy, gdy obie zadeklarują oczekiwanie przez
kolejnych czterdzieści jeden minut od przyjścia. Zauważmy, że otrzymane wielkości prawie nie różnią się od tych,
które otrzymaliśmy w modelu, w którym obie osoby mierzyły czas z dokładnością co do minuty (zob. tabela 3).
Uwaga. Im dokładniej obie osoby odmierzają czas wzajemnego oczekiwania na spotkanie w wyznaczonym miejscu, tym
szanse na spotkanie maleją. W pierwszym modelu, w którym obie mierzą czas z dokładnością co do kwadransa, szanse
na spotkanie przed upływem kwadransa wynoszą 62,5%. Gdy obie osoby mierzą czas z dokładnością do pięciu minut,
szanse na spotkanie w przeciągu kwadransa (trzech odcinków czasu po pięć minut) spadają do 50%. W trzecim modelu,
w którym mierzą czas z dokładnością co do minuty, szansa na spotkanie w przeciągu kwadransa (piętnastu odcinków o
długości jednej minuty każdy) spadają do 45%. Najmniejszą wartość − równą 43,8% - prawdopodobieństwo to osiąga w
modelu czwartym, w którym obie osoby bardzo dokładnie odmierzają sobie kwadrans, tj. 15 minut i zero sekund.
Uwaga ta − po chwili zastanowienia − nie dziwi: jeśli mierzymy czas z małą dokładnością (np. tak jak w modelu I z
dokładnością do kwadransa), jesteśmy skłonni tolerować u siebie samych i u znajomych większe spóźnienie łatwiej,
niż w przypadku, gdy czas mierzymy bardzo precyzyjnie − co do sekundy (jak w modelu IV).
Tabela 4. Wartości prawdopodobieństwa spotkania w przypadku, gdy obie osoby zadeklarują czas oczekiwania równy
60r minut po przyjściu na miejsce spotkania w modelu IV.
Wniosek. Jeśli obie osoby odmierzają czas oczekiwania z bardzo dużą dokładnością, to spotkanie dojdzie do
skutku z prawdopodobieństwem 50%, jeśli obie osoby zadeklarują, że poczekają co najmniej osiemnaście minut po
przyjściu. Natomiast prawdopodobieństwo to wzrośnie do 90% dopiero wtedy, gdy obie zadeklarują oczekiwanie przez
kolejnych czterdzieści jeden minut od przyjścia. Zauważmy, że otrzymane wielkości prawie nie różnią się od tych,
które otrzymaliśmy w modelu, w którym obie osoby mierzyły czas z dokładnością co do minuty (zob. tabela 3).
Uwaga. Im dokładniej obie osoby odmierzają czas wzajemnego oczekiwania na spotkanie w wyznaczonym miejscu, tym
szanse na spotkanie maleją. W pierwszym modelu, w którym obie mierzą czas z dokładnością co do kwadransa, szanse
na spotkanie przed upływem kwadransa wynoszą 62,5%. Gdy obie osoby mierzą czas z dokładnością do pięciu minut,
szanse na spotkanie w przeciągu kwadransa (trzech odcinków czasu po pięć minut) spadają do 50%. W trzecim modelu,
w którym mierzą czas z dokładnością co do minuty, szansa na spotkanie w przeciągu kwadransa (piętnastu odcinków o
długości jednej minuty każdy) spadają do 45%. Najmniejszą wartość − równą 43,8% - prawdopodobieństwo to osiąga w
modelu czwartym, w którym obie osoby bardzo dokładnie odmierzają sobie kwadrans, tj. 15 minut i zero sekund.
Uwaga ta − po chwili zastanowienia − nie dziwi: jeśli mierzymy czas z małą dokładnością (np. tak jak w modelu I z
dokładnością do kwadransa), jesteśmy skłonni tolerować u siebie samych i u znajomych większe spóźnienie łatwiej,
niż w przypadku, gdy czas mierzymy bardzo precyzyjnie − co do sekundy (jak w modelu IV).
|



 Model I
Model II
Model III
Model IV
Model V
Model VI
Model I
Model II
Model III
Model IV
Model V
Model VI






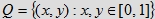
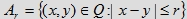 , gdzie
, gdzie