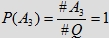Model I
Model II
Model III
Model IV
Model V
Model VI
Model I
Model II
Model III
Model IV
Model V
Model VI





|
Model I
Rozważmy sytuację, w której obie osoby posługują się zegarem mierzącym czas z dokładnością do kwadransa,
np. słuchają bicia zegara na wieży starego ratusza lub zegara kościelnego, który wybija pełne godziny i kwadranse:
 Niech
Niech
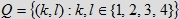 będzie zbiorem par kwadransów, w których przychodzą na spotkanie odpowiednio pierwsza i druga osoba, i niech
będzie zbiorem par kwadransów, w których przychodzą na spotkanie odpowiednio pierwsza i druga osoba, i niech
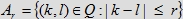 , gdzie , gdzie 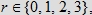 będzie zbiorem chwil przyjścia różniących się o nie więcej niż r kwadransów.
będzie zbiorem chwil przyjścia różniących się o nie więcej niż r kwadransów.
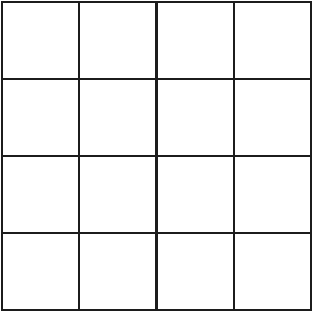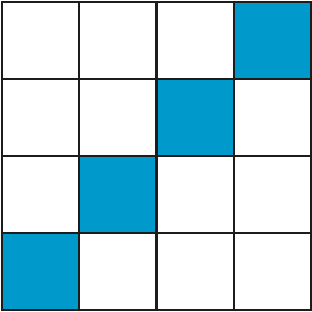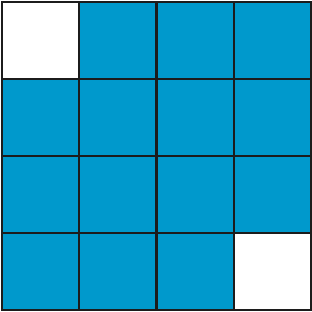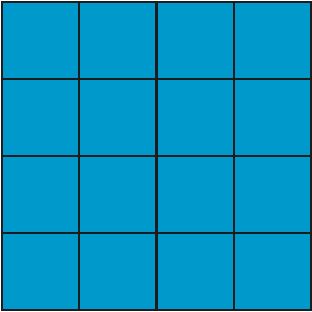 Animacja 3. Zbiór Q i jego podzbiór A0, A1, A2 i A3.
Oznaczmy symbolem #A liczbę elementów zbioru A. Zauważmy, że prawdopodobieństwo spotkania się osób mierzących czas
zegarem z dokładnością do kwadransa, z których każda czeka na drugą osobę tylko do końca kwadransa, w którym
przyszła (czyli w praktyce odchodzi z miejsca spotkania prawie zaraz po przyjściu), wyraża iloraz
Animacja 3. Zbiór Q i jego podzbiór A0, A1, A2 i A3.
Oznaczmy symbolem #A liczbę elementów zbioru A. Zauważmy, że prawdopodobieństwo spotkania się osób mierzących czas
zegarem z dokładnością do kwadransa, z których każda czeka na drugą osobę tylko do końca kwadransa, w którym
przyszła (czyli w praktyce odchodzi z miejsca spotkania prawie zaraz po przyjściu), wyraża iloraz
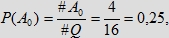 natomiast prawdopodobieństwo spotkania się osób czekających na siebie kwadrans po przyjściu, czyli do
wybicia kolejnego kwadransa po przyjściu, wyraża
natomiast prawdopodobieństwo spotkania się osób czekających na siebie kwadrans po przyjściu, czyli do
wybicia kolejnego kwadransa po przyjściu, wyraża
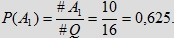 Z kolei liczby
Z kolei liczby
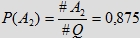 oraz oraz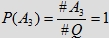 wyrażają prawdopodobieństwa spotkania się osób, gdy obie zadeklarują, że poczekają odpowiednio kolejne dwa
lub trzy kwadranse po przyjściu.
Zapiszmy te wartości prawdopodobieństwa w tabeli:
wyrażają prawdopodobieństwa spotkania się osób, gdy obie zadeklarują, że poczekają odpowiednio kolejne dwa
lub trzy kwadranse po przyjściu.
Zapiszmy te wartości prawdopodobieństwa w tabeli:
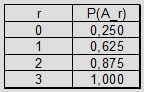 Tabela 1. Wartości prawdopodobieństwa spotkania w przypadku, gdy obie osoby zadeklarują czas oczekiwania
równy kwadransów po przyjściu na miejsce spotkania w modelu I.
Wniosek. Zauważmy, że spotkanie dojdzie do skutku z prawdopodobieństwem ponad 50%, jeśli obie osoby zadeklarują,
że poczekają co najmniej kolejny kwadrans po przyjściu. Natomiast szansa na spotkanie z prawdopodobieństwem ponad
90% ma miejsce dopiero wtedy, gdy obie zadeklarują oczekiwanie przez kolejne trzy kwadranse od przyjścia, czyli w
praktyce do wybicia pełnej godziny na zegarze.
Tabela 1. Wartości prawdopodobieństwa spotkania w przypadku, gdy obie osoby zadeklarują czas oczekiwania
równy kwadransów po przyjściu na miejsce spotkania w modelu I.
Wniosek. Zauważmy, że spotkanie dojdzie do skutku z prawdopodobieństwem ponad 50%, jeśli obie osoby zadeklarują,
że poczekają co najmniej kolejny kwadrans po przyjściu. Natomiast szansa na spotkanie z prawdopodobieństwem ponad
90% ma miejsce dopiero wtedy, gdy obie zadeklarują oczekiwanie przez kolejne trzy kwadranse od przyjścia, czyli w
praktyce do wybicia pełnej godziny na zegarze.
|



 Model I
Model II
Model III
Model IV
Model V
Model VI
Model I
Model II
Model III
Model IV
Model V
Model VI






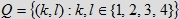
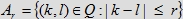 , gdzie
, gdzie 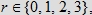
 Animacja 3. Zbiór Q i jego podzbiór A0, A1, A2 i A3.
Animacja 3. Zbiór Q i jego podzbiór A0, A1, A2 i A3.
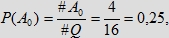
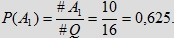
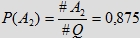 oraz
oraz