Archimedes (287 - 212 p.n.e.) udowodnił, że obszar okręgu o promieniu r jest równy polu trójkąta prostokątnego wysokości r i podstawie równej obwodowi koła. Użył do tego trzech pomocniczych twierdzeń, aby następnie używając dowodu nie wprost dowieść, że pole koła jest równe polu trójkąta.
Twierdzenie1:
Regularny ![]() może
być wpisany w okrąg.
może
być wpisany w okrąg.
Dowód:
Zaczynamy
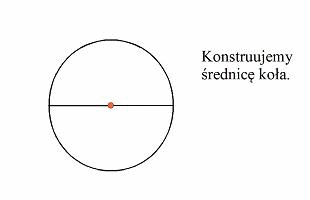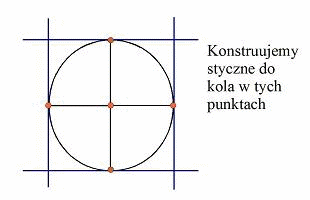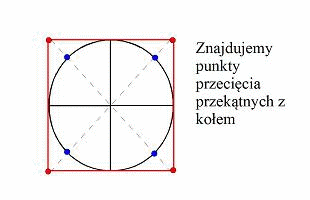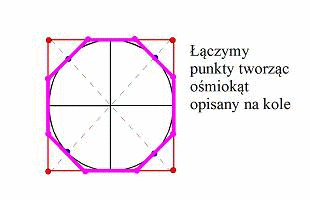
od wpisania kwadratu w koło![]() . Konstruujemy
średnice koła. Następnie konstruujemy
średnice,
która jest do niej prostopadła. Tworzymy punkty przedcięcia średnic z
kołem. Jeśli połączymy te punkty otrzymamy kwadrat wpisany wkoło.
Następnie używając wpisane
. Konstruujemy
średnice koła. Następnie konstruujemy
średnice,
która jest do niej prostopadła. Tworzymy punkty przedcięcia średnic z
kołem. Jeśli połączymy te punkty otrzymamy kwadrat wpisany wkoło.
Następnie używając wpisane![]() go
wkoło kwadratu wpisujemy ośmiokąt w
koło
go
wkoło kwadratu wpisujemy ośmiokąt w
koło![]() .Zaczynamy
od wpisania kwadratu wkoło, następnie tworzymy punkty dzielące boki
kwadratu ma połowy. Konstruujemy promienie przechodzące przez te
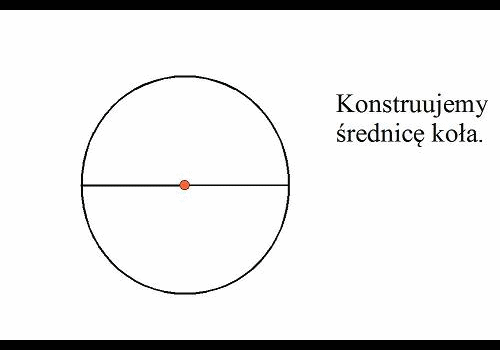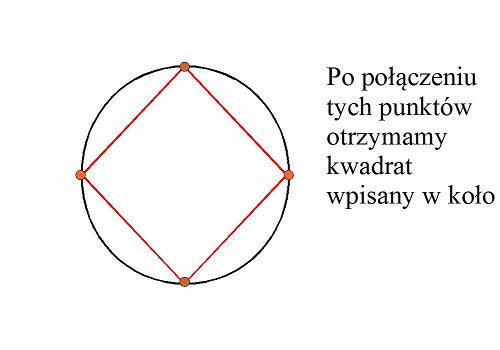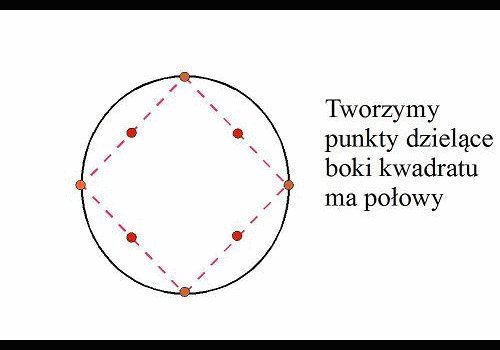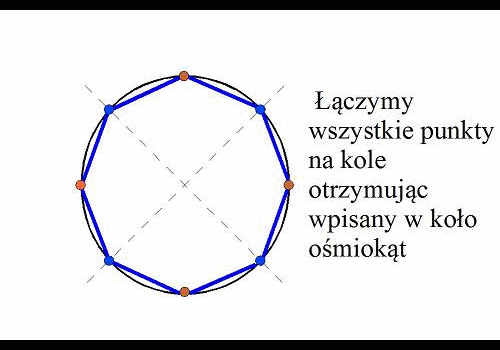
punkty. Potem tworzymy punkty przecięcia promieni z kołem. Wreszcie
łączymy wszystkie punkty na kole otrzymując wpisany w koło ośmiokąt.
.Zaczynamy
od wpisania kwadratu wkoło, następnie tworzymy punkty dzielące boki
kwadratu ma połowy. Konstruujemy promienie przechodzące przez te
punkty. Potem tworzymy punkty przecięcia promieni z kołem. Wreszcie
łączymy wszystkie punkty na kole otrzymując wpisany w koło ośmiokąt.
Ogólnie![]() ,
gdzie
,
gdzie![]() może
być wpisany w koło przez w pisanie w koło
może
być wpisany w koło przez w pisanie w koło ![]() , podzielenia jego
boków na połowy, przeprowadzenia przez otrzymane
punkty promieni koła oraz połaczenie wszystkich punktów na na brzegu
koła co prowadzi do otrzymania
, podzielenia jego
boków na połowy, przeprowadzenia przez otrzymane
punkty promieni koła oraz połaczenie wszystkich punktów na na brzegu
koła co prowadzi do otrzymania![]() .
.
Zauważmy,
że dla dużych n pole wpisanego jest
bliskie ale wciąż mniejsze niż pole koła.
Im
więcej boków ma wielokąt tym jego pole jest bardziej zbliżone do pola
koła.
Twierdzenie2:
Pole
regularnego wielokąta jest foremnego jest równe ![]() gdzie h prostopadła do ściany odległość
od środka figury, Q obwód
figury.
gdzie h prostopadła do ściany odległość
od środka figury, Q obwód
figury.
Dowód:
Obszar trójkąta to ![]() .
Regularny n-kąt ma n takich boków, a zatem n takich trójkątów.
Więc obszar regularnego n-kąta to
.
Regularny n-kąt ma n takich boków, a zatem n takich trójkątów.
Więc obszar regularnego n-kąta to ![]() .
Czyli
.
Czyli ![]()
gdzie
Q to obwód regularnego n-kata.