Jeśli funkcja f(x) jest ciągła w przedziale (a,b) oraz posiada oznaczoną pochodną (skończoną lub nieskończoną) wszędzie wewnątrz przedziału (a,b), to istnieje wewnątrz przedziału (a,b) liczba c taka, że f(b)-f(a)=f'(c)(b-a)
Interpretacja geometryczna
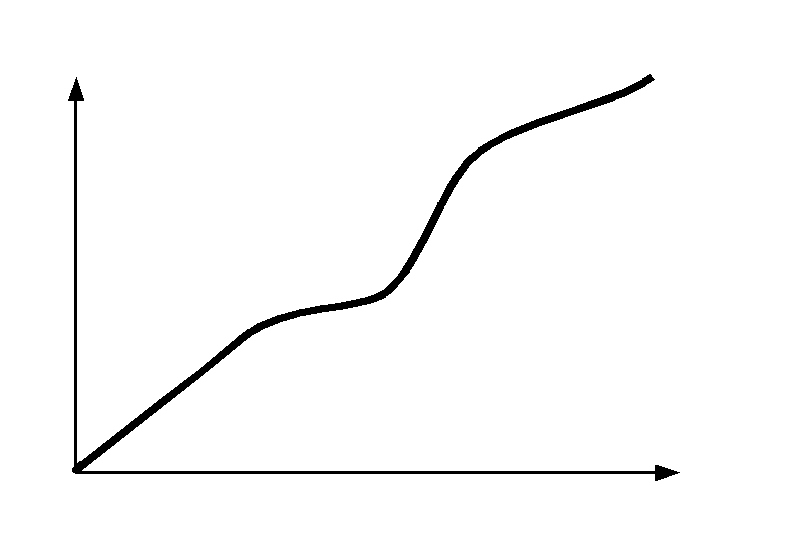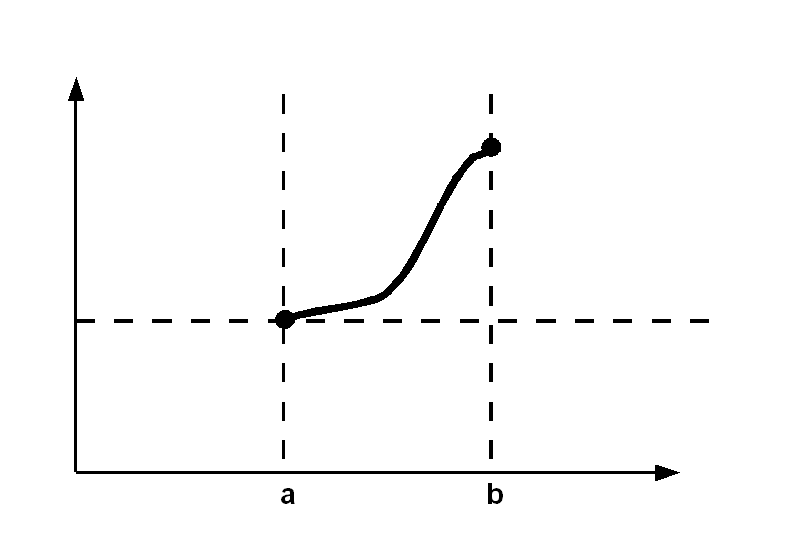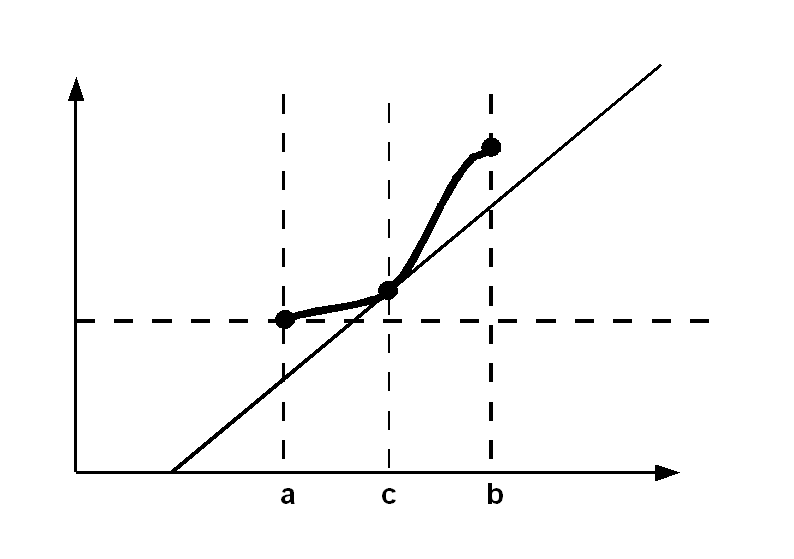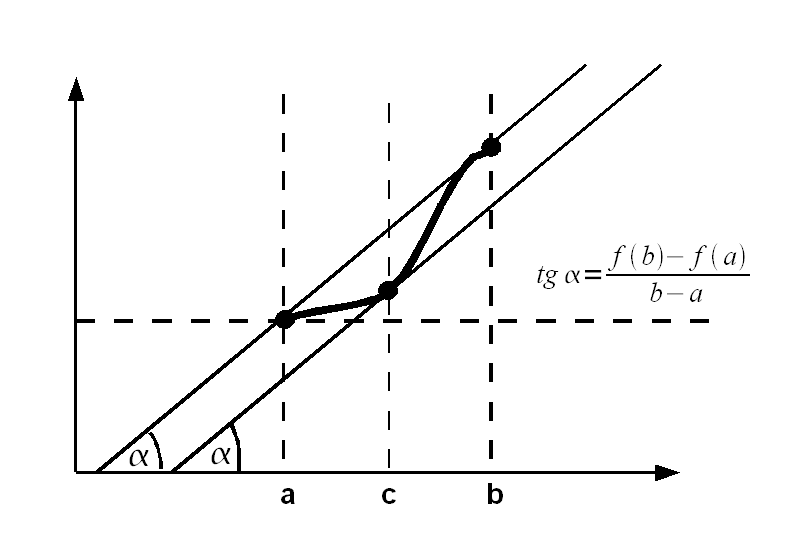
Twierdzenie Lagrange'a rozumiane geometrycznie, oznacza, że na łuku będącym wykresem funkcji od punktu (a,f(a)) do punktu (b,f(b)), istnieje punkt, którego styczna jest równoległa do prostej będzącej sieczną poprowadzoną między punktami (a,f(a)) i (b,f(b)). Współczynnik kierunkowy stycznej do wykresu funkcji w punkcie (c,f(c)) wynosi f'(c), co jest równe tangensowi kąta nachylenia stycznej do osi. Z twierdzenia Lagrange'a jest on r, równy pochodnej w tym punkcie: f'(c)=(f(b)-f(a))\(b-a)
Joseph Lagrange pochodził z Turynu, gdzie urodził się w
1736. W wieku 17 lat został wykładowcą matematyki w Królewskiej Szkole
Artyleryjskiej w Turynie. W roku 1757 założył wspólnie ze swoimi byłymi
uczniami Akademię Turyńską. Opierając się na pracach Eulera, Lagrange
opracował podstawowe pojęcia rachunku wariacyjnego oraz podał metodę
rozwiązywania problemów wariacyjnych. W roku 1772 Lagrange zostaje
członkiem Akademii Paryskiej i w 1787 roku wrócił do Paryża, gdzie
wykładał na wyższych uczelniach. W 1788 roku w swym klasycznym
traktacie Mechanika analityczna rozszerzył podstawy statyki i
mechaniki, podając ogólną formułę, znaną dziś jako zasada najmniejszego
działania. Lagrange w ciągu swojego życia ogłosił wiele prac z zakresu
analizy matematycznej (twierdzenie Lagrange'a i wnioski z niego
wypływające stanowią podstawy do badania tzw. przebiegu zmienności
funkcji, reszta Lagrange'a we wzorze Taylora), teorii liczb, algebry,
interpolacji