Funkcję zwaną
metryką można zdefiniować dla dowolnego (niepustego) zbioru X (nie
tylko dla 
).
W ten sposób będziemy mierzyć odległości między elementami dowolnego
zbioru X
Definicja [metryka, odległość]
Niech X będzie zbiorem niepustym, metryka w zbiorze X nazywamy dowolną funkcję
spełniającą następujące warunki:
Kule w
przestrzeniach metrycznych
-
-
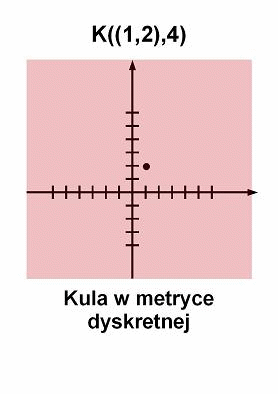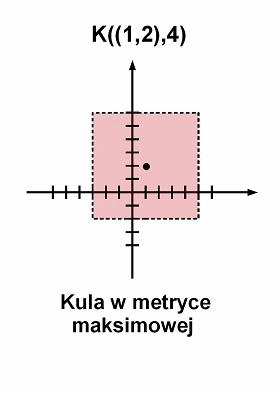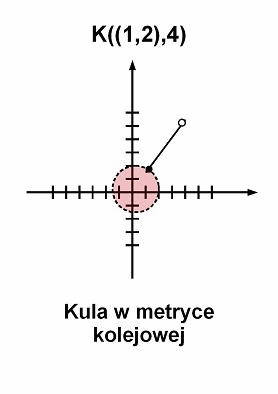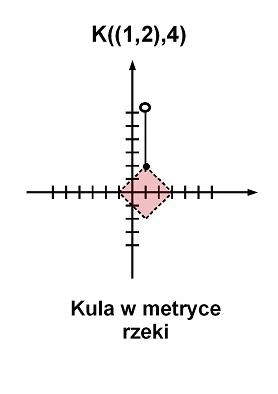
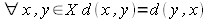(warunek
symetrii) -
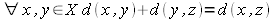(warunek trójkąta)
Parę (X,d) nazywamy przestrzenią metryczną. Dla dowolnych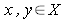
liczbę
d(x,y) nazywamy odległością punktów x i y oraz mówimy, że punkty x i y
są oddalone od siebie o d(x,y)
Metryka taksówkowa:
metryka
euklidesowa:
metryka maksimowa:
metryka dyskretna:
metryka rzeka:
metryka kolejowa:
metryka urzędu pocztowego:
Definicja [kula]
Niech d(x,y) będzie przestrzenią metryczną. Kulą o środku w punkcie 
i
promieniu 
nazywamy
zbiór: