Ślimak Teodorosa
,
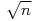dla 
,
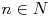gdy dany jest odcinek jednostkowy.Pomysł konstrukcji opiera się na twierdzeniu Pitagorasa. W tworzonym ciągu trójkątów, każdy kolejny ma jedną przyprostokątną długości 1, zaś drugą będącą przeciwprostokątną poprzedniego. Elementarne obliczenia, zilustrowane na obrazku, pozwalają stwierdzić, iż n-ty trójkąt w konstrukcji ma przeciwprostokątną długości
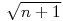.Nazwa konstrukcji pochodzi od greckiego matematyka i filozofa, Teodorosa z Cyreny. W oryginale konstrukcja kończyła się na
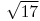, ponieważ
później ślimak zaczyna się "zawijać", tzn. kolejne trójkąty nakładają
się na poprzednio skonstruowane. Jednak oczywiście nie przeszkadza to
prowadzić konstrukcji dalej.Ciekawostka: W 1958 roku F. von E. Teuffel udowodnił, że niezależnie od długości konstrukcji, żadne dwie przeciwprostokątne różnych trójkątów w ciągu nigdy się nie pokryją.
Krok 1: Dany jest odcinek długości 1.
Krok 2: Konstruujemy odcinek prostopadły długości 1.
Krok 3: Łączymy końce odcinków i dostajemy trójkąt prostokątny o przeciwprostokątnej długości
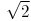.Krok 4: Konstruujemy odcinek długości 1, prostopadły do tej przeciwprostokątnej.
Krok 5: Łączymy i dostajemy trójkąt prostokątny o przeciwprostokątnej długości
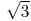.Powtarzamy kroki 4-5, otrzymując w kroku
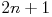odcinek
długości ,
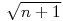dla 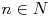.