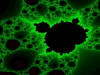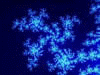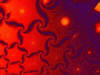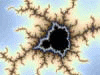
Fraktal to interesujący zbiór o ciekawej własności, mianowicie możemy wybrać z niego dowolnie mały fragment, a i tak będzie tak samo skomplikowany jak całość, ponieważ do złudzenia przypomina cały zbiór. nazywa się to "nieskończonym samopodobieństwem". mimo tego uzyskuje się je, powtarzając pewien prosty algorytm nieskończoną ilość razy. Pierwsze zdefiniowane matematycznie typowe przykłady fraktali to właśnie m.in.: zbiór Cantora i dywan Sierpińskiego.
Samo pojęcie fraktalu wprowadził w latach siedemdziesiątych XX wieku francuski informatyk i matematyk polskiego pochodzenia Benoit Mandelbrot.
Niektóre fraktale uzyskują naprawdę interesujący kształt dopiero po milionach powtórzeń danego schematu. Ciekawostką jest, że sto lat temu wielu matematyków uważało fraktale za "patologiczne" formy, ponieważ tak dalece odbiegały one od obowiązującego wówczas paradygmatu naukowego.

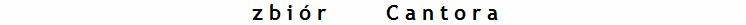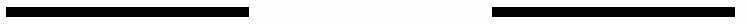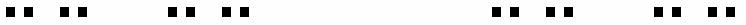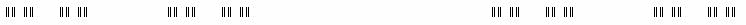
Zbiór Cantora to podzbiór przedziału domkniętego C0: = [0,1] w R wyznaczony indukcyjnie poprzez zstępujący ciąg zbiorów domkniętych (C0, C1, ...). zbiór Cn jest sumą 2n zbiorów domkniętych.
tworzenie zbioru Canotra: odcinek [0,1] dzielimy na trzy równe odcinki (środkowy jest otwarty, a dwa skrajne są domknięte), usuwamy środkowy odcinek, następnie każdy z powstałych odcinków domkniętych traktujemy tak samo, dzieląc go na trzy i wyrzucając ten środkowy, itd.