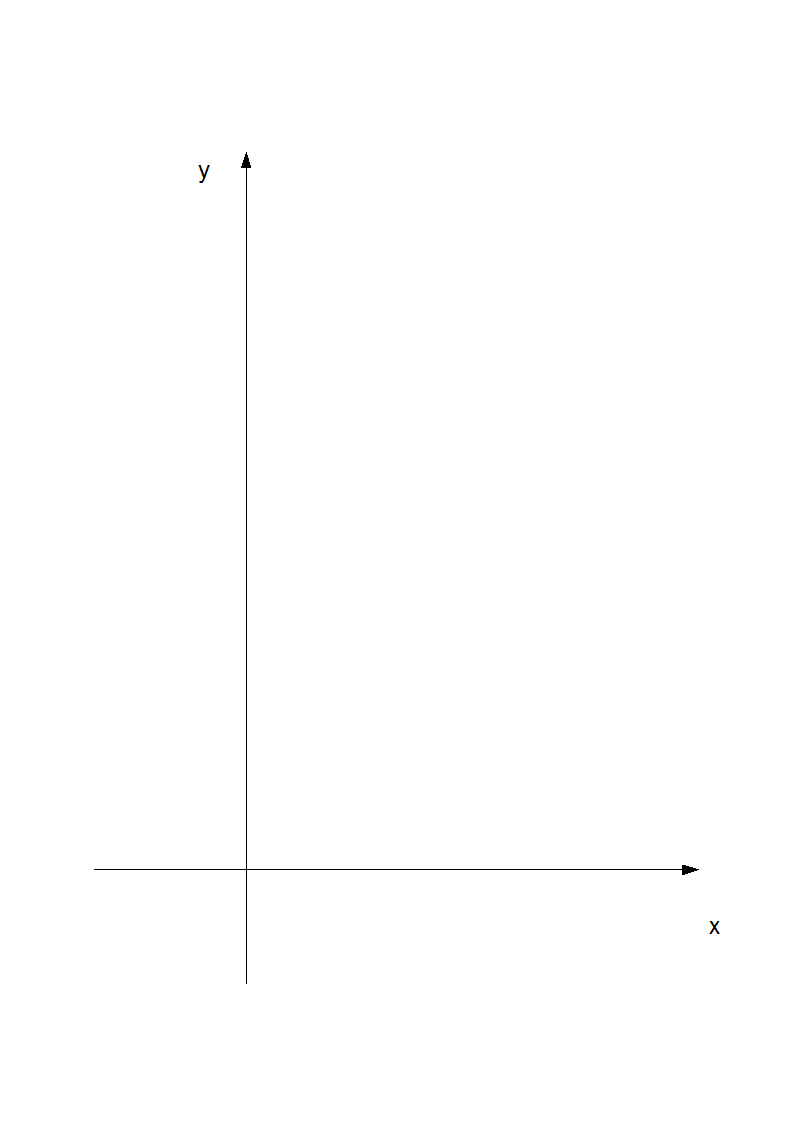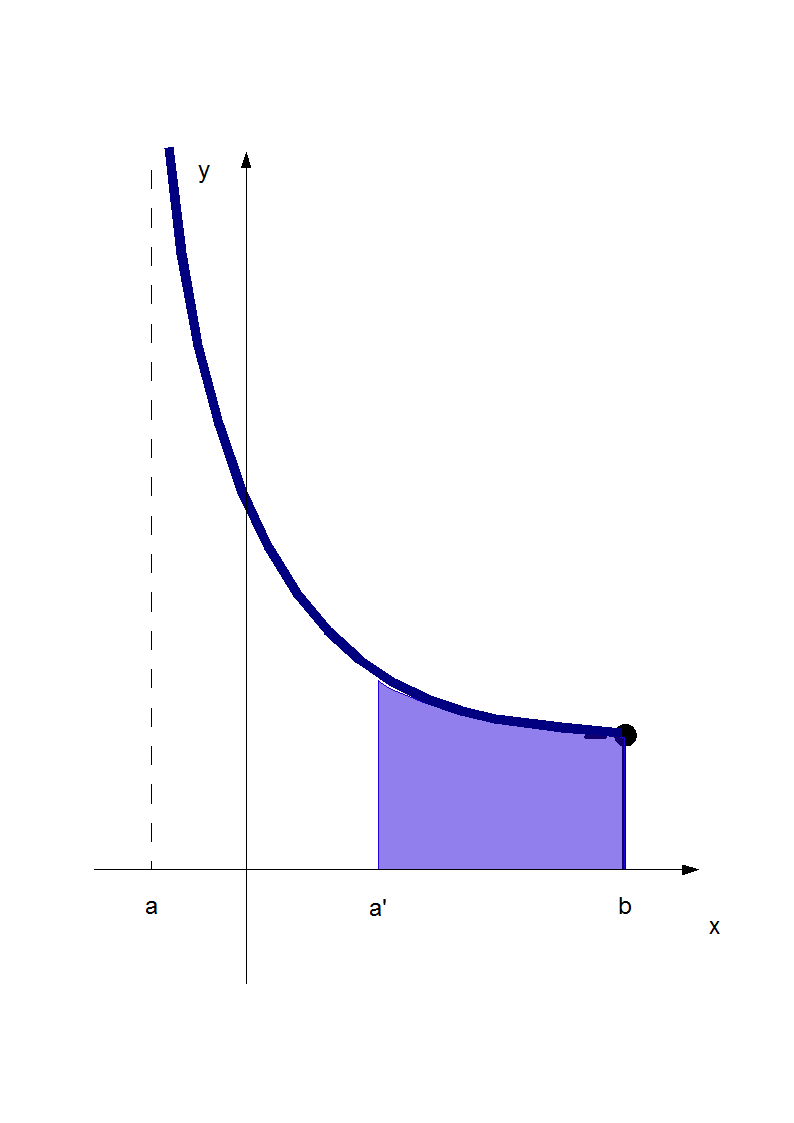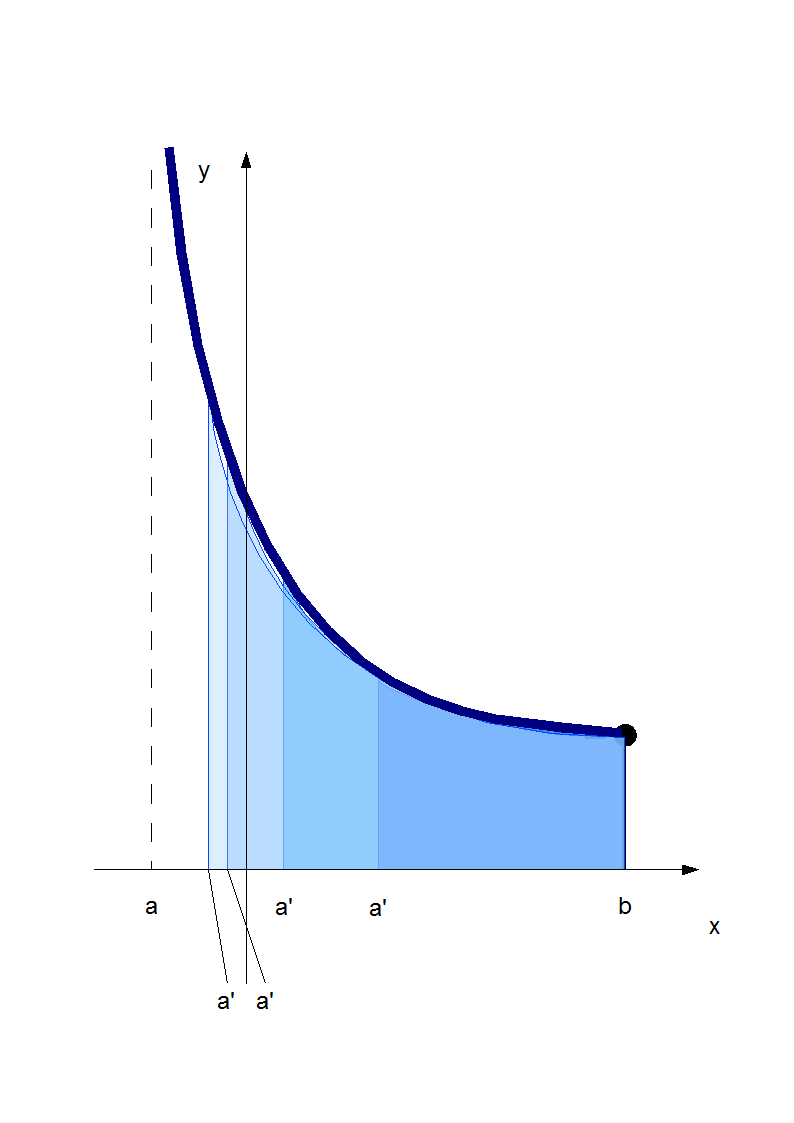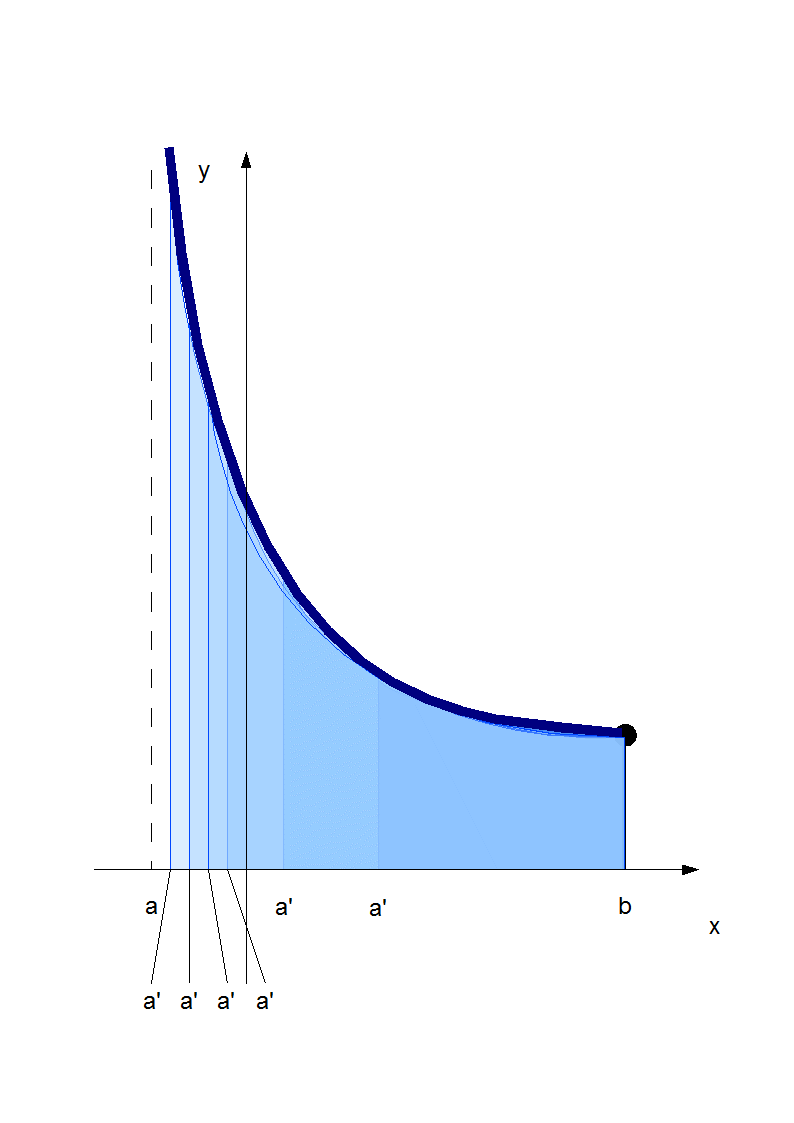
(1)
Niech 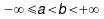 oraz niech
oraz niech 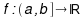 będzie
funkcją.
Przez całkę niewłaściwą funkcji f na przedziale (a,b] rozumiemy
będzie
funkcją.
Przez całkę niewłaściwą funkcji f na przedziale (a,b] rozumiemy
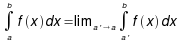
o ile całki Riemanna po prawej stronie oraz granica po prawej stronie istnieją.
(2)
Niech 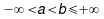 oraz niech
oraz niech 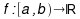 będzie
funkcją.
Przez całkę niewłaściwą funkcji f na przedziale [a,b) rozumiemy
będzie
funkcją.
Przez całkę niewłaściwą funkcji f na przedziale [a,b) rozumiemy
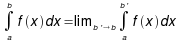
o ile całki Riemanna po prawej stronie oraz granica po prawej
stronie istnieją.
Gdy całka niewłaściwa 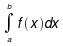 istnieje,
to mówimy,
że całka jest zbieżna
(w przeciwnym razie mówimy, że całka jest rozbieżna).
Jeśli całka niewłaściwa
istnieje,
to mówimy,
że całka jest zbieżna
(w przeciwnym razie mówimy, że całka jest rozbieżna).
Jeśli całka niewłaściwa 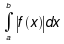 istnieje to mówimy, że całka jest bezwzględnie zbieżna
(oczywiście zbieżność bezwzględna całki implikuje zbieżność
całki).
istnieje to mówimy, że całka jest bezwzględnie zbieżna
(oczywiście zbieżność bezwzględna całki implikuje zbieżność
całki).
Przykłady:
(1) Całka niewłaściwa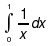 jest rozbieżna, bo
jest rozbieżna, bo 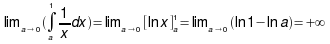
(2) Całka niewłaściwa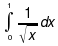 jest zbieżna i równa 2, gdyż
jest zbieżna i równa 2, gdyż 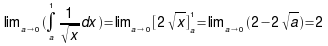
(1) Całka niewłaściwa
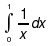 jest rozbieżna, bo
jest rozbieżna, bo 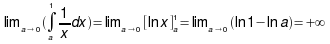
(2) Całka niewłaściwa
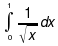 jest zbieżna i równa 2, gdyż
jest zbieżna i równa 2, gdyż