Krzywa stożkowa - zbiór punktów powstałych na przecięciu stożka i płaszczyzny.
Krzywe stożkowe są nazywane inaczej krzywymi drugiego stopnia , gdyż można je w kartezjańskim układzie współrzędnych opisać równaniem algebraicznym drugiego stopnia względem obu zmiennych x i y.
Istnieje kilka szczególnych przypadków, kiedy pomimo przecięcia stożka płaszcyzną nie otrzymamy krzywej stożkowej:
- prosta - gdy płaszczyzna tnąca pokrywa się z tworzącą
- parę przecinających się prostych - gdy oś stożka jest zawarta w płaszczyźnie tnącej równoległej do osi stożka
- punkt - gdy płaszczyzna tnąca jest styczną do wierzchołka bądź podstawy
Wyróżnia się następujące krzywe stożkowe, zależnie od kąta, jaki tworzy płaszczyzna przecinająca z osią stożka i jego tworzącą:
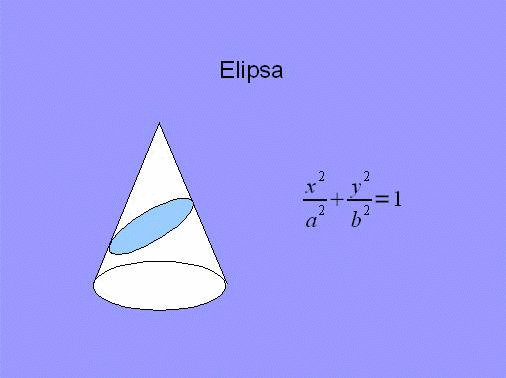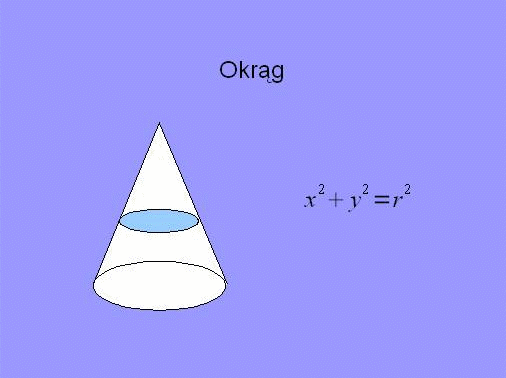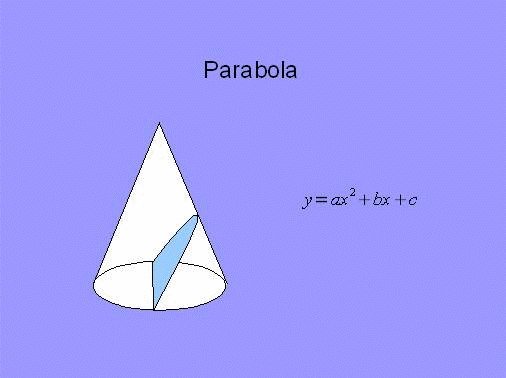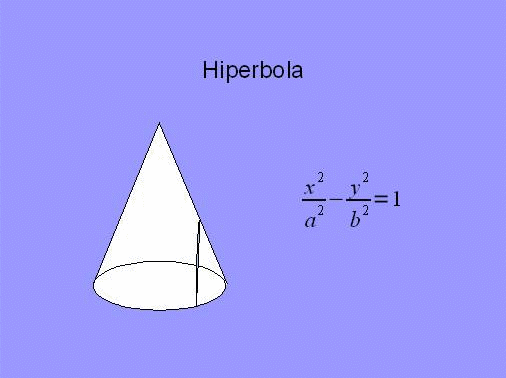
- elipsa - gdy kąt pomiędzy płaszczyzną
przecinającą a osią stożka jest większy od kąta między tworzącą a osią
stożka,
- okrąg - szczególny przypadek dla
elipsy; powstaje, gdy wspomniany kąt jest prosty, czyli płaszczyzna
tnąca jest prostopadła do osi stożka,
- parabola - jeżeli kąt pomiędzy
płaszczyzną tnącą a osią stożka jest równy kątowi pomiędzy osią stożka
a jego tworzącą, czyli tworząca jest równoległa do płaszczyzny tnącej,
- hiperbola - Jeżeli kąt pomiędzy
płaszczyzną tnącą a osią stożka jest mniejszy od kąta pomiędzy osią
stożka a jego tworzącą; powstaje również, gdy płaszczyzna tnąca jest
równoległa do osi stożka, ale nie obejmuje tej osi.