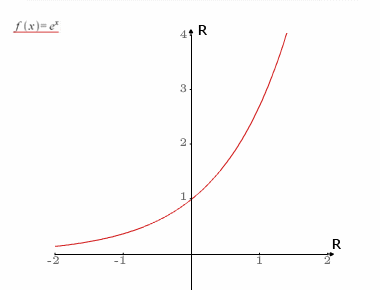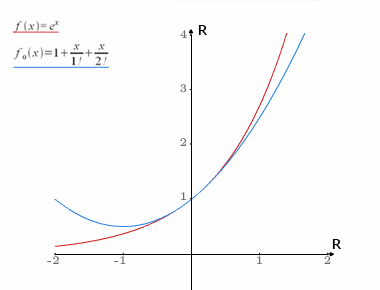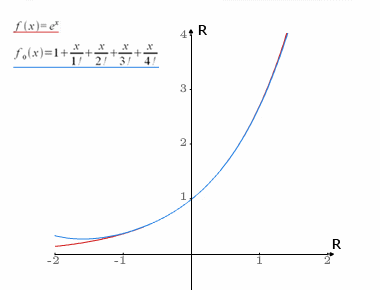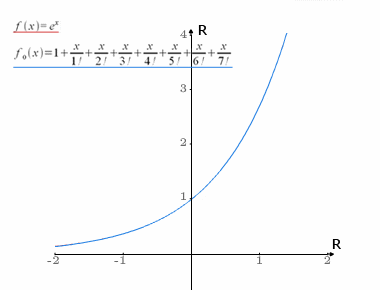
Aproksymacja funkcji
 sumami szeregu Taylora
sumami szeregu Taylora
Aproksymowanie funkcji może polegać na przybliżaniu jej za pomocą kombinacji liniowej tzw. funkcji bazowych. Od funkcji aproksymującej, przybliżającej zadaną funkcję nie wymaga się, aby przechodziła ona przez jakieś konkretne punkty,Mówi się że funkcja przybliżająca wygładza daną funkcję (gdy funkcja jest gładka, jest też różniczkowalna). Przybliżenie takie powoduje pojawienie się błędów, zwanych błędami aproksymacji. Dużą zaletą aproksymacji w stosunku do interpolacji jest to, że aby dobrze przybliżać, funkcja aproksymująca nie musi być wielomianem bardzo dużego stopnia (w ogóle nie musi być wielomianem) - Przybliżenie w tym wypadku rozumiane jest jako minimalizacja pewnej funkcji błędu. Najpopularniejszą miarą tego błędu jest średni błąd kwadratowy, ale możliwe są również inne funkcje błędu, jak choćby średni błąd.
Odkrywcze i w efekcie bardzo istotne w uchwyceniu zagadnienia o aproksymacji funkcji jest twierdzenie Taylora, które w sposób bardzo obrazowy przedstawia działanie przybliżania funkcji.
Twierdzenie Taylora
Niech Y będzie przestrzenią unormowaną. Załóżmy, że
 jest (n+1)-razy różniczkowalna na [a,b] w sposób
ciągły. Wówczas dla każdego
jest (n+1)-razy różniczkowalna na [a,b] w sposób
ciągły. Wówczas dla każdego 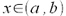
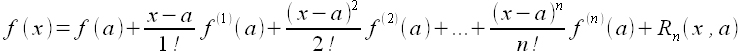
gdzie
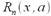 spełnia warunek
spełnia warunek 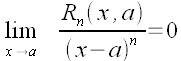
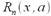 nazywamy resztą (Peano) we wzorze
Taylora. Jeśli a = 0, to wzór Taylora nazywamy wzorem Maclaurina.
nazywamy resztą (Peano) we wzorze
Taylora. Jeśli a = 0, to wzór Taylora nazywamy wzorem Maclaurina.Przybliżanie funkcji przy pomocy wzoru Taylora ma charakter lokalny, tzn. odnosi się jedynie do wybranego punktu a. Jeżeli w zastosowaniach pojawia się potrzeba mówienia o innych wartościach, to zakłada się o nich najczęściej że są dostatecznie bliskie punktu a. Sensowne wydaje się jednak pytanie o to kiedy wielomian ze wzoru Taylora przybliża funkcję ze z góry zadaną dokładnością - w tym celu potrzebne jest dokładniejsze oszacowanie reszty lub po prostu wyrażenie jej w sposób jawny.
Reszty we wzorze Taylora wyrażone w sposób jawny
W przypadku gdy
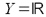 resztę we wzorze Taylora
można wyrazić w sposób jawny. Oto niektóre ze znanych przedstawień
reszty:
resztę we wzorze Taylora
można wyrazić w sposób jawny. Oto niektóre ze znanych przedstawień
reszty:Reszta w postaci całkowej
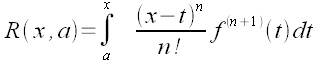
Reszta w postaci Lagrange'a
Istnieje takie
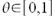 , że
, że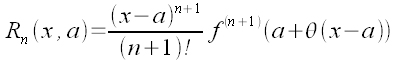 .
.Lub inaczej, istnieje takie
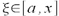 , że
, że .
.Uwaga: W tym przypadku założenie, że
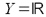 nie jest istotne.
nie jest istotne.Reszta w postaci Cauchy'ego
Istnieje takie
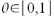 , że
, że
Szacowanie reszty
Jeżeli
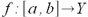 jest (n+1)-krotnie różniczkowalna
oraz istnieje takie
jest (n+1)-krotnie różniczkowalna
oraz istnieje takie 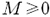 , że
, że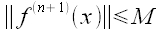 dla
dla 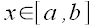 ,
, to dla reszty
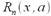 we wzorze Taylora dla f
mamy oszacowanie
we wzorze Taylora dla f
mamy oszacowanie 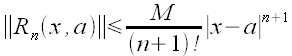 dla
dla 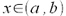 .
.Jeżeli natomiast ,
 jest n-krotnie
różniczkowalna oraz
jest n-krotnie
różniczkowalna oraz 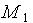 jest taką liczbą, że
jest taką liczbą, że 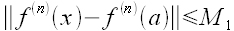 dla
dla 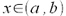 ,
, to dla reszty
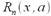 we wzorze Taylora dla f
mamy oszacowanie
we wzorze Taylora dla f
mamy oszacowanie 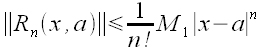 dla
dla 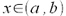 .
.Szereg Taylora
Jeśli funkcja
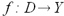 , gdzie
, gdzie 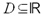 , tak jak poprzednio, jest przestrzenią
unormowaną, ma w punkcie
, tak jak poprzednio, jest przestrzenią
unormowaną, ma w punkcie 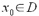 pochodne dowolnego
rzędu, to można rozważać szereg
pochodne dowolnego
rzędu, to można rozważać szereg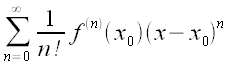 ,
, gdzie przyjęto
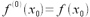 . Szereg ten nazywamy szeregiem
Taylora funkcji f. Jeżeli
. Szereg ten nazywamy szeregiem
Taylora funkcji f. Jeżeli 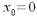 , to
szereg ten nazywamy szeregiem Maclaurina.
, to
szereg ten nazywamy szeregiem Maclaurina.Przy założeniu istnienia pochodnych dowolnego rzędu funkcji
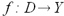 w punkcie
w punkcie 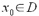 , warunkiem
koniecznym i wystarczającym na to, aby dla danego
, warunkiem
koniecznym i wystarczającym na to, aby dla danego 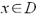 szereg Taylora funkcji f był zbieżny do f(x)
jest, aby ciąg
szereg Taylora funkcji f był zbieżny do f(x)
jest, aby ciąg 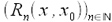 reszt we wzorze Taylora był
zbieżny do zera.
reszt we wzorze Taylora był
zbieżny do zera.Szereg (wzór) Taylora jest efektywnym narzędziem aproksymacji funkcji dostatecznie dużo razy różniczkowalnych. Często do obliczenia przybliżonej wartości funkcji (o wartościach rzeczywistych), liczy się wartość dla m-tej sumy częściowej jej szeregu Taylora. Tak więc przybliżoną wartość funkcji rzeczywistej f, spełniającej powyższe założenia można znaleźć licząc kilka pierwszych wartości:
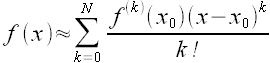 ,
, przy czym błąd jest wtedy nie większy niż:
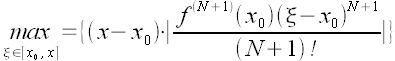 .
.Aproksymacje można wykorzystać w sytuacji, gdy nie istnieje funkcja analityczna pozwalająca na wyznaczenie wartości dla dowolnego z jej argumentów, a jednocześnie wartości tej nieznanej funkcji są dla pewnego zbioru jej argumentów znane. Można wówczas zastosować jedną z wielu metod aproksymacyjnych. Potrzeba przybliżenia danej funkcji inną funkcją pojawia się w wielu zadaniach. Może mieć np. zastosowanie przy obliczaniu funkcji standardowych lub wtedy, gdy funkcja jest zdefiniowana bardzo skomplikowanym wzorem. Jednym z najczęstrzych ze sposobów rozwiązania tego zadania jest przybliżanie funkcji sumami częściowymi ich rozwinięć w szeregi Taylora.