Pojęcie wymiaru, pomimo pozornej prostoty, sprawiało matematyką sporo problemów. Intuicyjne definiowanie wystarczało dla obiektów, które można było zobaczyć, lecz okazywało się niewystarczające przy bardziej teoretycznych rozważaniach. Jedna z pierwszych prób jednoznacznego zdefiniowania brzmiała:

Definicja:

Wymiar zbioru A dany jest indukcyjnie:

1. Jeżeli zbiór A jest zbiorem pustym, to jego wymiar równy jest -1
2. Jeżeli dowolny podzbiór zbioru A można odseparować od reszty zbioru zbiorem B o wymiarze n oraz istnieje podzbiór zbioru A, którego nie można odseparować od reszty zbioru zbiorem C o wymiarze mniejszym od n, to zbiór A ma wymiar n+1.

Jak w praktyce wygląda stosowanie tej definicji? Zbiór pusty ma wymiar -1. Punkt, ponieważ żaden zbiór nie może go podzielić, ma wymiar równy 0. Prosta, okrąg i dowolna krzywa mogą zostać podzielone na części przy użyciu punktów, zatem ich wymiar równy jest 1. Jak widać definicja ta jest zgodna z intuicją oraz umożliwia badanie zbiorów dowolnego wymiaru. Jej wady to konieczność badania wszystkich możliwych podzbiorów i indukcyjne rozumowanie. Jednak w roku 1883 Georg Cantor przedstawił problem, który zobrazował prawdziwe braki powyższej definicji

Definicja:



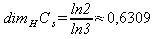
Geometryczna interpretacja przedstawiona jest na rysunku powyżej. Gdzie tkwi problem? W dowolnym momencie konstrukcji otrzymujemy sumę skończenie wielu odcinków, zatem zbiór o wymiarze równym 1. Jednak zbiór Cantora składa się tylko z pojedyńczych, odseparowanych punktów, czyli jego wymiar wynosi 0. Intuicyjna definicja nie pozwala na odróżnienie obiektów zachowywujących się "porządnie" od tych, które zmieniają swój wymiar. Rozwiązanie tego problemu zostało zaproponowane dopiero w pierwszej połowie XX wieku przez Felixa Hausdorffa. Przyjęta przez niego definicja pozwala na istnienie obiektów o wymiarze nie będącym liczbą całkowitą, a nawet wymierną. Dla zbioru Cantora jest on równy: