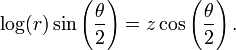WSTĘGA
MÖBIUSA
OPIS
Wstęga
Möbiusa to dwuwymiarowa
zwarta rozmaitość topologiczna istniejąca w przestrzeni
trójwymiarowej, którą można uzyskać sklejając taśmę
końcami
"na odwrót". Jej najważniejszą cechą jest to, że ma
tylko jedną stronę (jest tzw. powierzchnią
jednostronną).
Posiada
również tylko jedną krawędź - "sklejenie" tej krawędzi
(niemożliwe w przestrzeni trójwymiarowej) daje butelkę Kleina.
Opisana przez niemieckiego matematyka
Augusta Möbiusa i Johanna
Benedicta Listinga w 1858 roku.
Przykład
wstęgi Möbiusa to prostokątny pasek papieru, skręcony o 180
stopni, a następnie sklejony końcami. Opisywany jest jako przykład
powierzchni jednostronnej. Błędnie uznaje się, że symbol
nieskończoności pochodzi od wstęgi Möbiusa; symbol ten był w
użyciu od ponad dwustu lat, gdy Möbius i Listing odkryli wstęgę.
WSTĘGA
MÖBIUSA
JAKO
OBIEKT W GEOMETRII I TOPOLOGII
Jednym ze sposobów
przedstawienia wstęgi Möbiusa jako podzbioru  jest następująca
parametryzacja:
jest następująca
parametryzacja:
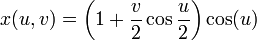
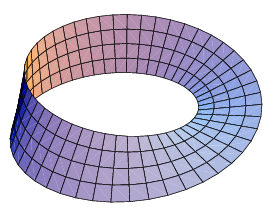


gdzie 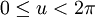 oraz
oraz 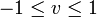 .
W ten sposób tworzy się wstęga Möbiusa o szerokości 1,
której
środkowe koło leżące na płaszczyźnie x-y ma
promień 1 i jest
wyśrodkowane w punkcie (0,0,0). Parametr u
przebiega dookoła wstęgi a parametr v od jednej krawędzi do
drugiej. W cylindrycznym układzie
współrzędnych (r,θ,z)
nieograniczona wersja wstęgi Möbiusa może być przedstawiona jako
równanie
.
W ten sposób tworzy się wstęga Möbiusa o szerokości 1,
której
środkowe koło leżące na płaszczyźnie x-y ma
promień 1 i jest
wyśrodkowane w punkcie (0,0,0). Parametr u
przebiega dookoła wstęgi a parametr v od jednej krawędzi do
drugiej. W cylindrycznym układzie
współrzędnych (r,θ,z)
nieograniczona wersja wstęgi Möbiusa może być przedstawiona jako
równanie
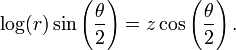
- Topologicznie wstęga
Möbiusa może być zdefiniowana jako kwadrat [0,1] × [0,1], w
którym górna i dolna krawędź są utożsamione przez relację
(x,0)
~ (1-x,1),
jak pokazuje to rysunek po prawej
WSTĘGA
MÖBIUSA
W SZTUCE

Bardzo
szybko stała się popularnym motywem zdobniczym i inspiracją dla
wielu artystów. Było wśród nich także sporo
matematyków, którzy
(jak Cliff Long) twierdzili:
„..rzeźbienie
sprawia, że radykalnie lepiej rozumiem pojęcie powierzchni i
matematykę, jaka się w nim kryje.”
Powrót do strony zbiorczej
autor: Bożena
Gręda (II
rok - IM UJ)
 jest następująca
parametryzacja:
jest następująca
parametryzacja:
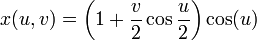



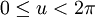 oraz
oraz 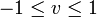 .
W ten sposób tworzy się wstęga Möbiusa o szerokości 1,
której
środkowe koło leżące na płaszczyźnie x-y ma
promień 1 i jest
wyśrodkowane w punkcie (0,0,0). Parametr u
przebiega dookoła wstęgi a parametr v od jednej krawędzi do
drugiej. W cylindrycznym układzie
współrzędnych (r,θ,z)
nieograniczona wersja wstęgi Möbiusa może być przedstawiona jako
równanie
.
W ten sposób tworzy się wstęga Möbiusa o szerokości 1,
której
środkowe koło leżące na płaszczyźnie x-y ma
promień 1 i jest
wyśrodkowane w punkcie (0,0,0). Parametr u
przebiega dookoła wstęgi a parametr v od jednej krawędzi do
drugiej. W cylindrycznym układzie
współrzędnych (r,θ,z)
nieograniczona wersja wstęgi Möbiusa może być przedstawiona jako
równanie