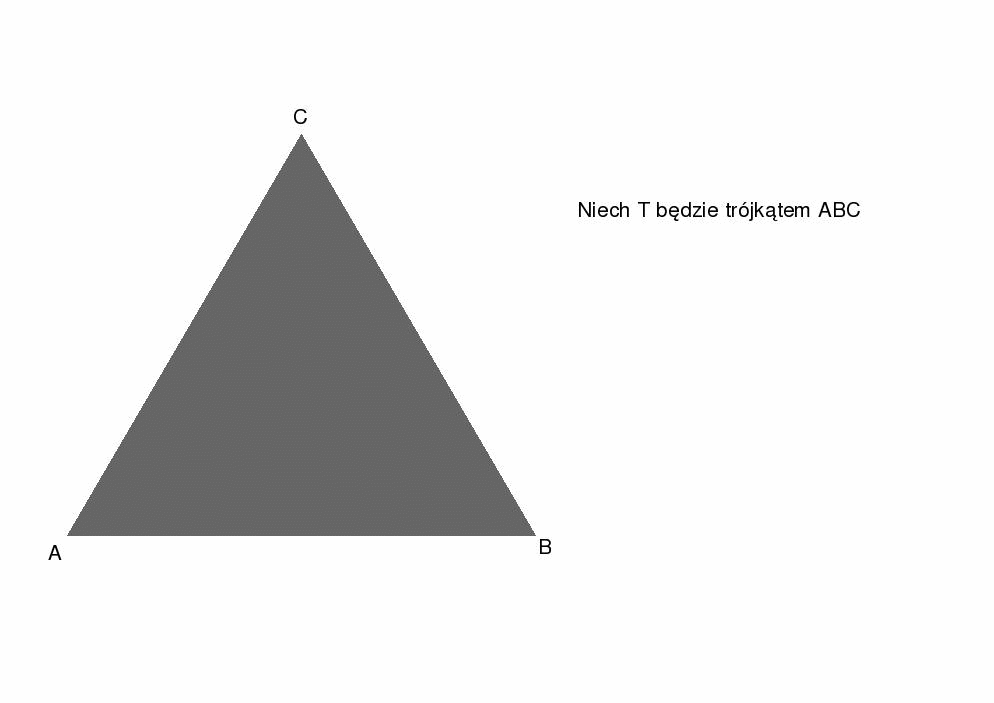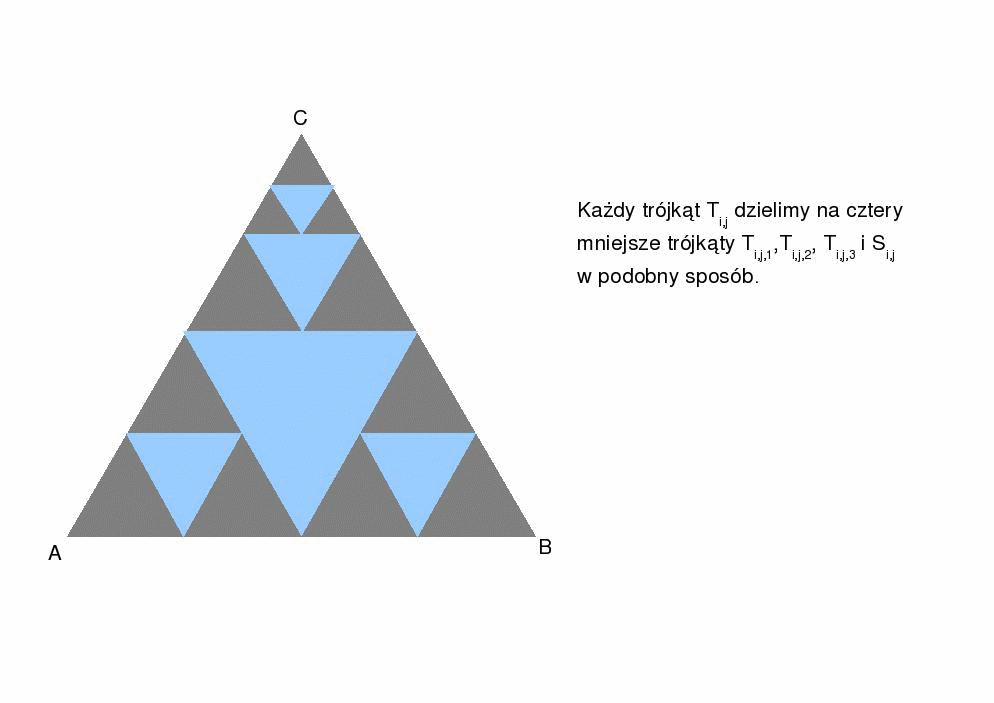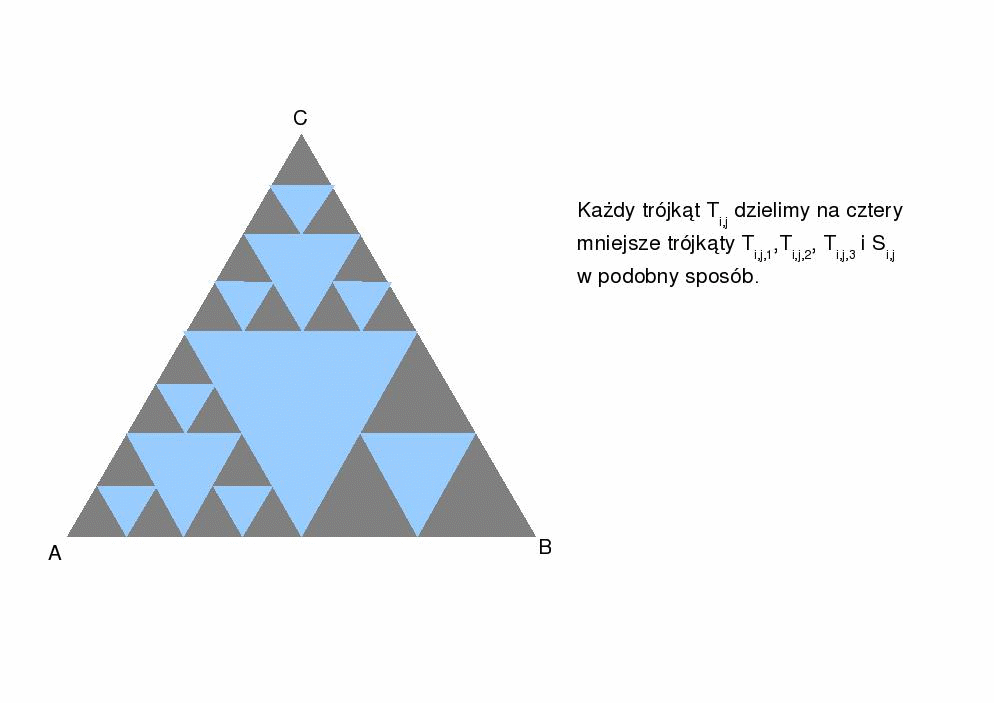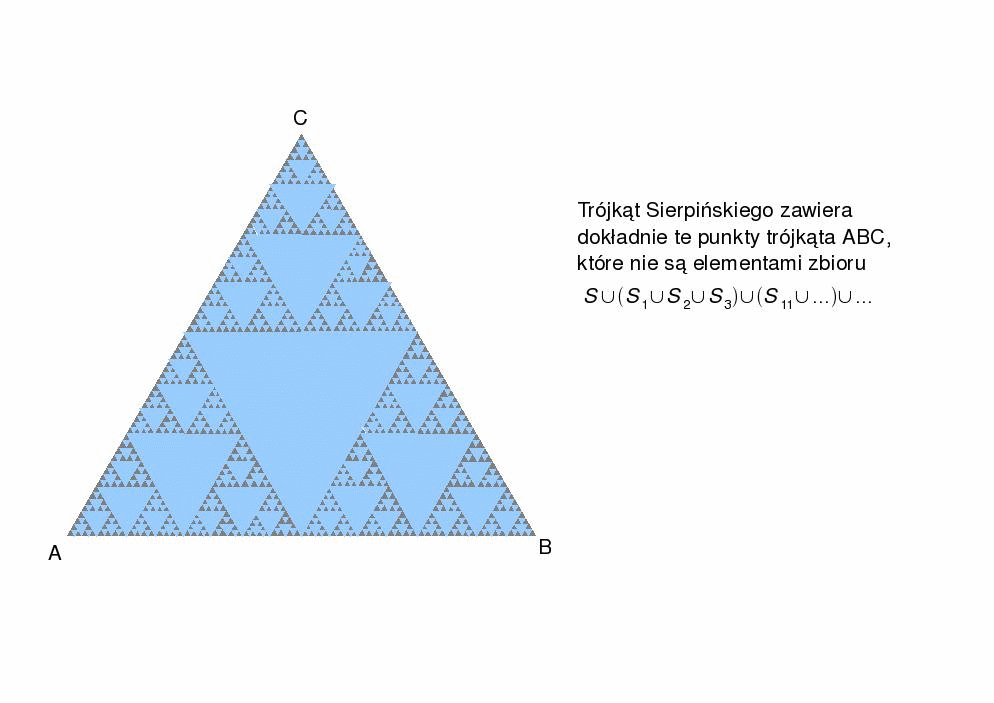
TRÓJKĄT SIERPIŃSKIEGO


1.  KONSTRUKCJA TRÓJKĄTA SIERPIŃSKIEGO:

a) Rysujemy trójkąt równoboczny ABC, np. o długości 1. Środki boków tego trójkąta łączymy odcinkami. Dzielimy trójkąt na cztery mniejsze trójkąty T1,T2,T3 i S. Środki         krawędzi trójkąta ABC są wierzchołami trójkąta S. Traktujemy S jako zbiór otwarty, a zbiory Ti : i=1,2,3, jako zbiory domknięte. Tym sposobem otrzymujemy zbiory                 rozłączne S i .
b) Każdy z trójkątów Ti, tzn. T1,T2,T3 dzielimy na cztery mniejsze, tj. Ti,1,Ti,2,Ti,3 i Si, wyznaczając środki boków trójkątów T1,T2,T3 i łączymy je odcinkami.
c) Każdy z trójkątów Ti,j, tzn,Ti,1,Ti,2,Ti,3 dzielimy na cztery mniejsze, tj. Ti,j,1,Ti,j,2,Ti,j,3 i Si,j.
          d) Powtarzamy poprzednie czynności rekurencyjnie, aż do nieskończoności. W rezultacie otrzymujemy trójkąt Sierpińskiego, przy czym Ttrójkąt Sierpińskiego zawiera                        dokładnie te elementy zbioru ABC, które nie są elementami zbioru :
Trójkąt Sierpińskiego
2. WŁASNOŚCI:     
                         
Pole trójkąta Sierpińskiego
 0
Wymiar fraktalny
 ln3/ln2=1,585...
Klasyfikacja
 zbiór fraktalny
                                            
3. UWAGI, CZYLI CHAOS POTRAFI BYĆ "PORZĄDNY":

       Trójkąt Sierpińskiego, możemy otzrymać przy pomocy tzw. "gry w chaos". Mianowicie wybieramy na płaszczyźnie trzy dowolne niewspólniowe punkty 1, 2, 3. Wybieramy kolejny punkt płaszczyzny, nazywamy go punktem gry (P). Wybieramy losowo jeden z pkt. 1, 2, lub 3 i stawiamy punkt pomiędzy wybranym punktem i punktem P. Oznaczamy ten punkt jako P1. Ponownie wybieramy losowo jeden z pkt. 1,2,3 i wyznaczamy srodek odległości między wybranym punktem a punktem P1. Oznaczamy go P2. Powtarzamy czynność rekurencyjnie. W efekcie, zakładając, że punkty były losowane z mniej więcej jednakowym prawdopodobieństwem jest pewien wariant trójkąta Sierpińskiego, którego wierzchołkami są punkty 1,2,3.

autor: Kamila Bara (II rok - IM UJ)



Powrót do strony zbiorczej