Krzywa Lissajous
Krzywa parametryczna opisująca drgania harmoniczneWZÓR:
x(t)=A.sin(at+δ) , y(t)=B.sin(bt)
Jedną z metod uzyskiwania krzywych Lissajous jest podanie na wejścia oscyloskopu, pracującego w trybie XY, dwóch sygnałów sinusoidalnych o częstotliwościach pozostających w stosunku a/b.
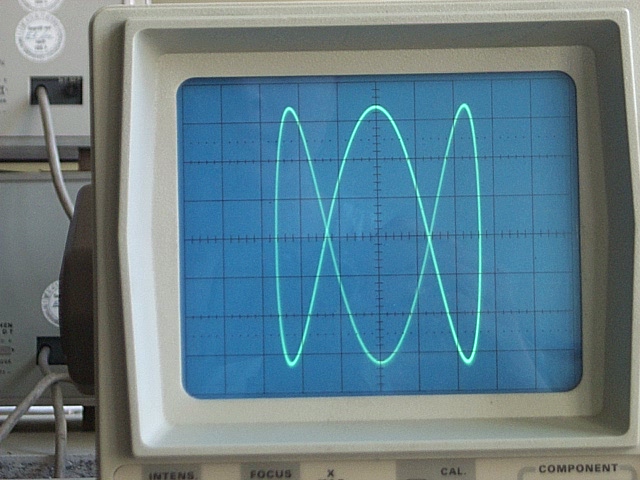
Kształt krzywych jest szczególnie uzależniony od współczynnika a/b. Dla współczynnika równego 1, krzywa jest elipsą, ze specjalnymi przypadkami okrąg (A = B, δ = π/2 radianów) oraz odcinek (δ = 0). Inne wartości współczynnika dają bardziej złożone krzywe, które są zamknięte tylko gdy a/b jest liczbą wymierną.
