Twierdzenie Napoleona i nie tylko...
                                                                                                                                    Każdy trójkąt posiada punkt nazywany środkiem ciężkości. Powstaje on w miejscu przecięcia się środkowych trójkąta, czyli odcinków łączących środki boków z przeciwległymi bokami.
   Napoleon, który co cię pewnie zaskoczy bardzo cenił sobie matematykę, miał kiedyś taki oto problem do rozwiązania: "Weżmy dowolny trójkąt, na jego bokach wybudujmy trójkąty równoboczne, wyznaczmy środki ciężkości nowo powstałych trójkątów, połączmy je i zaobserwujmy czym będzie nowo powstała figura."
   Na początku, dla ułatwienia, niech wyjściowy trójkąt też będzie równoboczny. Weź kartkę i ołówek (pióro też może być jeżeli nie masz żadnego ołówka pod ręką :) i konstruuj razem ze mną:
   1. Za pomocą cyrkla (zapomniałem wcześniej o nim wspomnieć a niestety jest konieczny) zbudujmy trójkąt równoboczny.
   2. Na jego bokach tym samym sposobem zbudujmy kolejne trzy trójkąty równoboczne (na pewno zauważyłeś, że na każdym boku mogą powstać dwa trójkąty, ale zajmijmy się tylko tymi, które są "na zewnątrz" wyjściowego trójkąta.
   3. Wyznaczmy środki przynajmniej dwóch boków każdego nowego trójkąta.
   4. Połączmy powstałe punkty z przeciwległymi wierzchołkami tworząc środkowe.
   5. Oznaczmy przecięcia środkowych jako środki ciężkości i połączmy je.
   Teraz sprawdż czy wyszło nam to samo:

 (jeżeli animacje nie uruchomiają się same - co nie powinno się zdarzyć - należy na nie kliknąć)		                                                                                                                    
   Czy i tobie wyszedł trójkąt równoboczny? Przypadek? Może. Sprawdźmy więc co powstanie jeżeli za trójkąt wyjściowy weźmiemy trójkąt równoramienny. Najpierw spróbuj samemu wykonując wszystkie korki prócz pierwszego tak jak ostatnio (jak narysować trójąt równoramienny chyba ci nie muszę mówić). Potem porównaj wynik z moim:
   Znowu trójkąt równoboczny. To chyba nie jest przypadek. A może się pomylliśmy? Miejmy nadzieję że nie i sprawdżmy co będzie dla trójkąta prostokątnego.
   Znowu? Ale może powstaje on tylko w tych trzech przypadkach? Co będzie jeżeli weźmiemy trójkąt rozwatrokątny:
   lub ostrokątny (pamiętaj aby najpierw samemu spróbować wykonać rysunek):
   No teraz to już moglibyśmy stwierdzić, że zawsze będzie to trójkąt równoboczny. Ale czy na pewno? Może otzrymany trójkąt tylko go przypomina, a wcale nie ma równych boków. Sprawdźmy więc długości boków i kąty między nimi. Ja sprawdzę na swoich rysunkach, a ty na swoich (jeśli jednak ich nie wykonałeś sprawdzaj razem ze mną).
   Tak więc nasz trójkąt jes tna 100% trójkątem równobocznym niezależnie od kształtu wyjściowego trójkąta. Ale dlaczego tak się dzieje? W matemtyce jest już tak, że nie wystarczy coś zauważyć, ale trzeba to udowdnić.
Podobno sam Napoleon (tak, TEN Napoleon) opracował dowód tej zależności i stąd nazwa tego twierdzenia - twierdzenie Napoleona. Czy jest to prawda? Nie wiadomo, ale jest to prawdopodobne, ponieważ cesarz Francji prócz podbijaniem innych narodów w wolnych chwilach poświęcał także sporo czasu na rozwiązywanie różnych problemów matematycznych.
   Dowód, który przedstawię, nie jest jednak na pewno dziełem Napoleona, ponieważ opracował go w 1997 roku Piotr Danilewski, uczeń jednej z krakowskich szkół podstawowych. Więc jeżeli uważasz, że twoja wiedza matematyczna wykracza poza szkołę podstwawową zastanów się chwilę i spróbuj samemu wpaść na sposób w jaki to udowodnić. Jeżeli jedank po prostu ci się nie chce albo po wielogodzinnym wytężeniu mózgu na nic nie wpadłeś (nie przejmuj się, mi też się nie udało) obejrzyj animację poniżej.
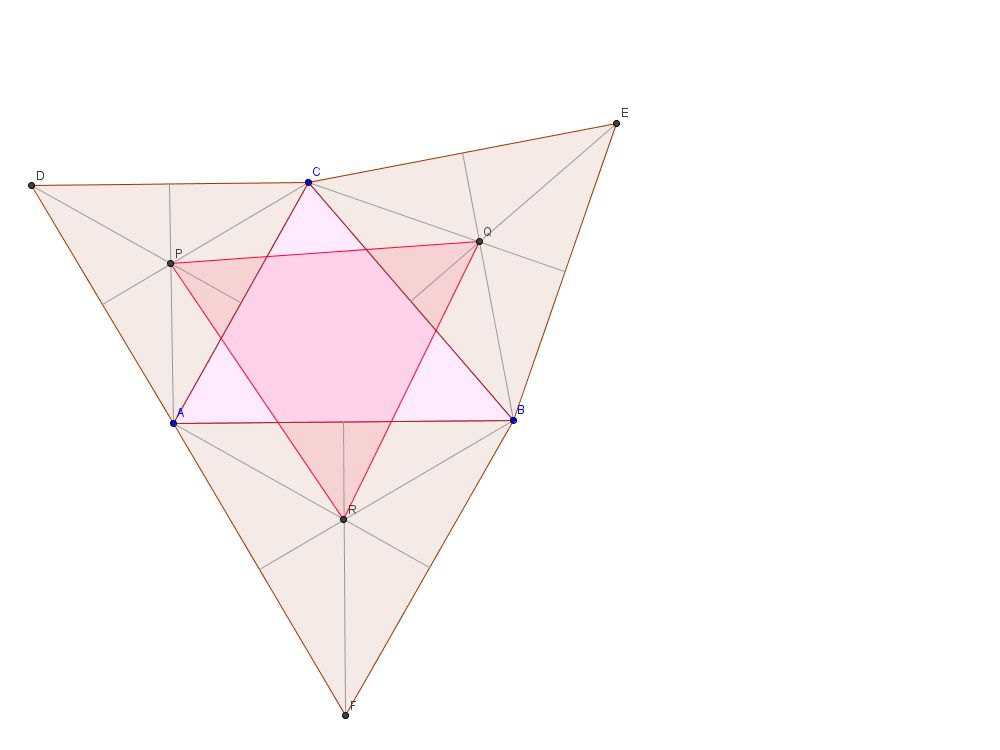
   Udowodniliśmy właśnie twierdzenie Napoleona, więc myślisz pewnie wnioskując z tytułu, że zajmiemy się teraz "nie tylko". Oto i one:
   Jak zapewnie dobrze wiesz, trójkąt posaida cztery interesujące punkty:
   - środek okegu opisanego na trójkącie - powstaje przez przecięcie się symetralnych (prostych przechodzących przez środki boków trójkąta i do nich prostopadłych)
   - środek okegu wpisanego w trójkąt - powstaje przez przecięcie się dwusiecznych kątów trójkąta
   - ortocentrum - powstaje przez przecięcie się prostych zawierających wysokości trójkąta
   - i już wczesniej omawiany środek ciężkości - w interpretacji geometrycznej przecięcie dwusiecznych trójkąta
   W trójkącie równobocznym wszystkie one znajdują się w tym samym miejscu - nazwijmy go punktem S.
   Porównajmy teraz cztery opisane wyżej punkty trójkąta wyjściowego z punktem S trójkata równobocznego. Jak myślisz, czy zobaczymy coś ciekawego? Przekonaj się konstruując wszytskie punkty i porównując je albo patrz jak ja to robię.
   Jako Śc oznaczmy środek ciężkości, OO - środek okręgu opisanego, OW - okręgu wpisanego, Orto - ortocentrum.
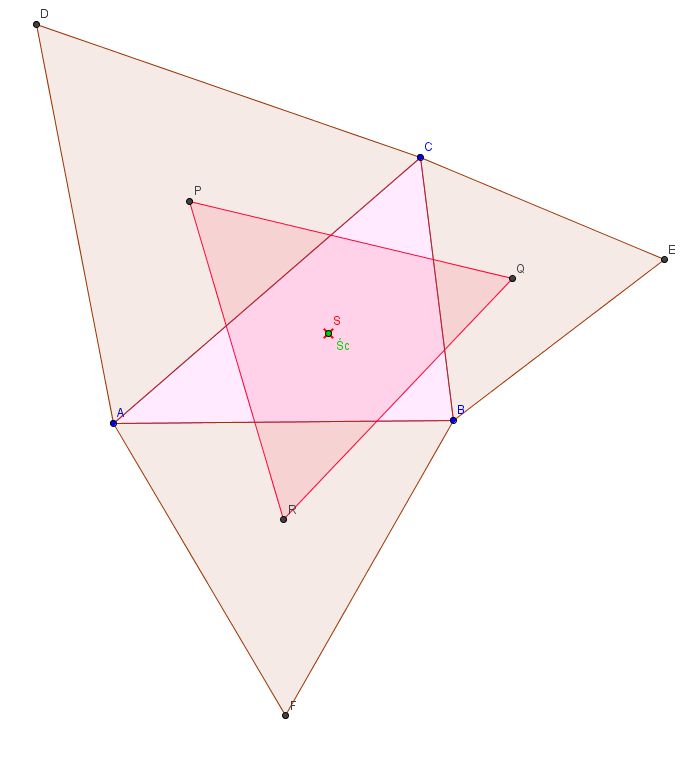
   Tak jak się pewnie spodziewałeś dwa punkty pokrywają się - są to środek ciężkości i S. Upewnijmy się i sprawdźmy czy te punkty zawsze są położone w tym samym miejscu.
   Jak widać Napoleon przegapił jedną ciekawą zależność. A może ją znalazł a nie umiał udowodnić? Sprawdźmy czy my umiemy.
   Słyszałeś kiedyś o dowodzie analitycznym? Jeśli nie, patrz uważnie; jeżeli tak to też patrz i pilnuj abym nie popełnił błędu.
   Narysujmy trójkąt i układ współrzędnych tak aby jeden bok leżał na osi x, a pozostały jeden wierzchołek na osi y, tak jak na rysunku poniżej (da się tak ustawić każdy trójkąt). Punkt A ma wspórzędne (a,0), B(b,0) i C(0,c).
   Następnie dorysujmy trzy trójkąty równoboczne na bokach i skonstruujmy trójkąt równoboczny z ich środków ciężkości. Współrzędne punktów E można wyliczyć z układu dwóch równań: pierwszego na okrąg o środku C i promieniu |CB| a drugiego także na okrąg o tym samym promieniu ale o środku w punkcie B. Po krótkich przekształceniach, których wykonanie pozostawiam ciekawskiemu czytelnikowi dostajemy dwie współrzędne (jak już wcześniej wspominałem na każdym boku mogą powstać dwa trójkąty równoboczne czyli dwa różne punkty E). Sprawdzając ich położenie w układzie współrzędnych eliminujemy jedne i pozstaje:
   Punkty D i F otrzymamy przez podmienienie odpowiednich niewiadomych.
   Jeżeli nie dokońca się orientujesz co na razie się stało nie przejmuj się bo teraz nadchodzi ta najważniejsza część dowodu i zarazem łatwiejsza.
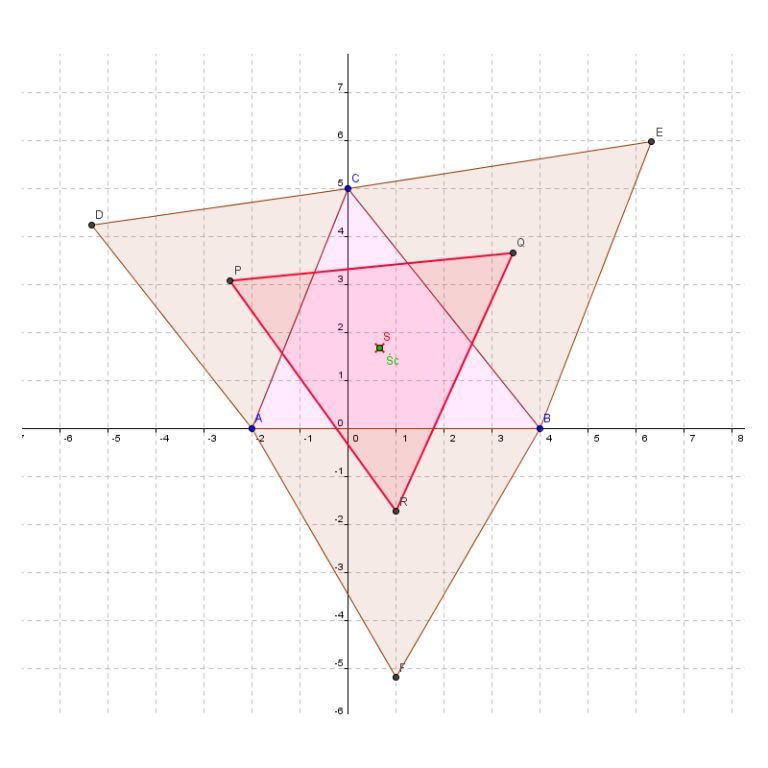
   Wcześniej wspominałem o interpretacji geometrycznej środka masy. Istnieje również interpretacja algebraiczna, tj. każda ze współrzędnych środka masy jest średnią arytmetyczną odpowiednich współrzędnych wszystkich wierzchołków trójkąta (czyli o dziwo trzech). Czyli bierzemy współrzędną x-ową pierwszego wierzchołka, dodajemy do niej wspłółrzędną x-ową drugiego i analogicznei trzeciego i otzrymaną sumę dzielimy przez 3. Dostalismy właśnie pierwszą współrzędną środka masy tego trójkąta. Analogicznie postępujemy ze współrzędnymi y-owymi. Więc zanim przejdziemy dalej mam dla ciebie małe ćwiczenie: oblicz współrzędne środka masy trójkąta o wierzchołkach w punktach (0.1), (1,0) i (2,2).
   Jeżeli wyszło ci (7,4) to znaczy że popełniłeś błąd bo prawidłowym rozwiązaniem jest punkt (1,1).
   Tak więc możemy w analogiczny sposób policzyć współrzędne środków masy wszystkich trzech trójkątów:
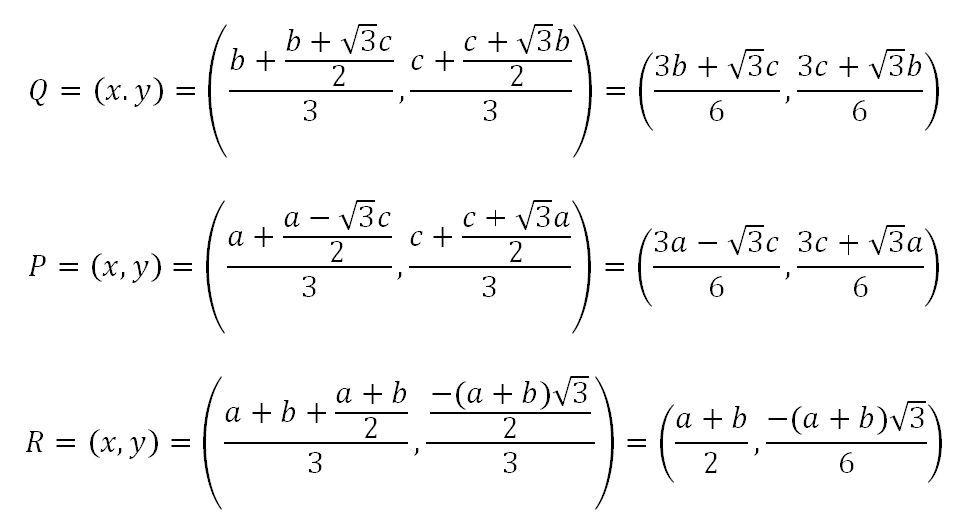
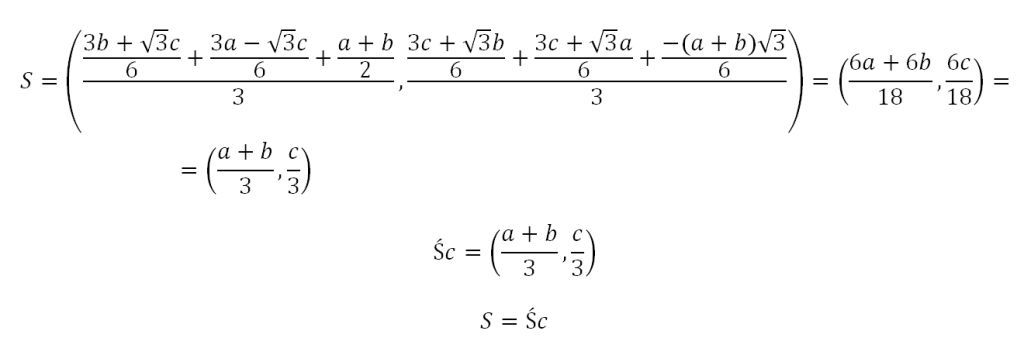
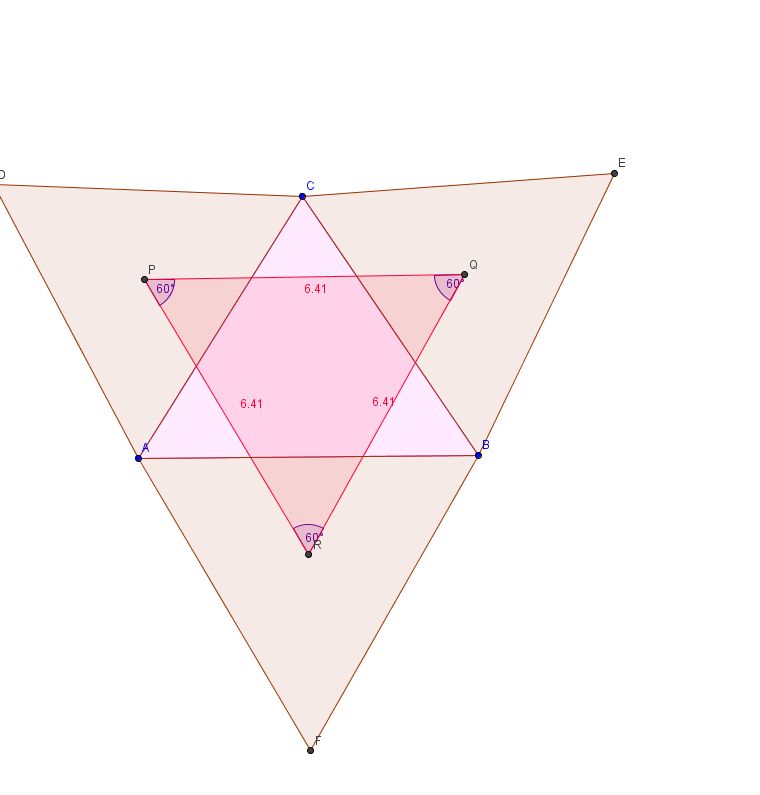
   Punkt S jest zarazem środkiem ciężkości trójkata QPR więc analogicznei można wyliczyć jego współrzędne i porównać ze współrzędnymi środka ciężkości trójkąta ABC:
   Tak więc wygląda dowód analityczny. Może się to wydawać trochę skomplikowane ale wystarczy, że samemu spróbujesz to zrobića, a wszystko powinno stać się jasne.
   Tak więc udowdniliśmy, że środki ciężkości tych dwóch trójkątów zawsze się pokryją. A co by było gdybyśmy zamiast punktów PQR w trójkąt połączyli punkty DEF ?
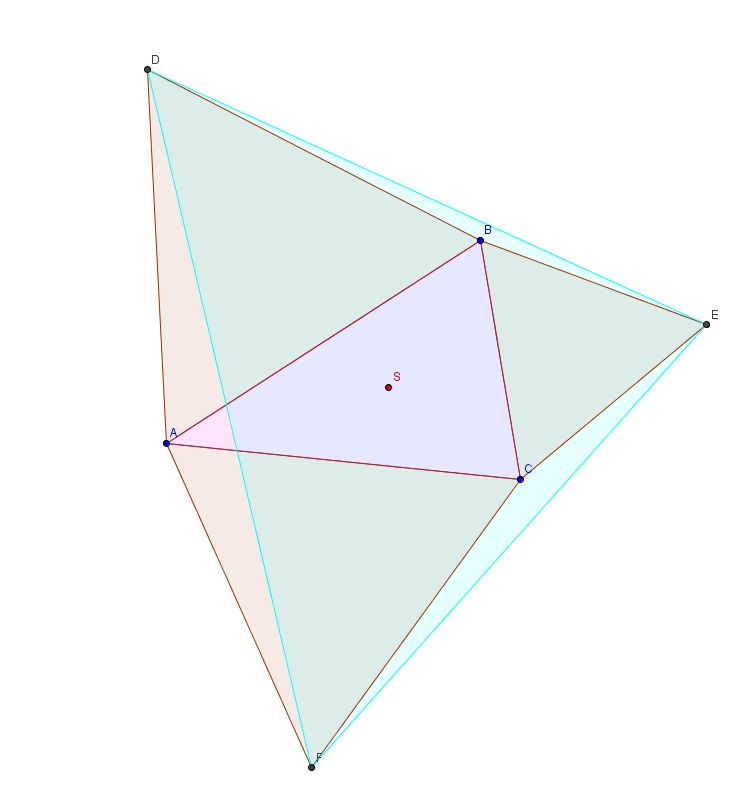
   Jak mogłeś zauważyć trójkąt DEF nie jest już zawsze równoboczny. A co ze środkiem ciężkości? Weź myszkę, uruchom Geogebrę albo jakiś inny program geometryczny i sprawdź samemu czy punkty bedą się pokrywać.
   Deja vu? Tą zależność można udowdnić analogicznie do poprzedniej, tylko zamiast brać punkty P Q R jako wierzchołki trójkąta tym razem są nimi D E F. Ale to już pozostawiam tobie.
   Trójkąt z trójkątami równobocznymi wybudowanymi na jego bokach ma jeszcze jedną ciekawą własność - punkt Torriciellego - Fermata. Powstaje on na przecięciu odcinków DC, AE i BF. Czy umiesz znaleźć jakieś zależności pomiędzy tymi trezma odcinkami? Oto co ja znalazłem:
   Tak więc długości tych odcinków są takie same i są nachylone do siebie zawsze pod kątem 60 stopni. Czy to wszytskie zależności? Nie wiem, ale jeżeli cię zainteresowałem mam nadzieję że samemu spróbujesz jeszcze czegoś poszukać.
   A gdyby zmodyfikować problem Napoleona i zamiast trójkatów równobocznych na bokach trójkata wyjściowego wybudować trójkąty podobne? Tak jak poprzednio zacznijmy od trójkata równobocznego. Tak więc weź ołówek, kartkę i co tam jeszcze masz, co mogłoby się przydać i konstruuj razem ze mną:
   1. Narysuj trójkat równoboczny.
   2. Skonstruuj na jednym z jego boków dowolny trójkąt.
   3. Przenosząc długości boków skonstruuj pozostałe dwa trójkaty tak aby wszystkie trzy stykały się z wyjściowym trójkatem tą samą krawędzia.
   4. Powtórz tą operację dla róznych trójkątów podobnych.
   Oto co mi wyszło: (pierwsza animacja stwarzanie trójkąta PQR, druga - kształt PQR w zależności od trójkątów podobnych)
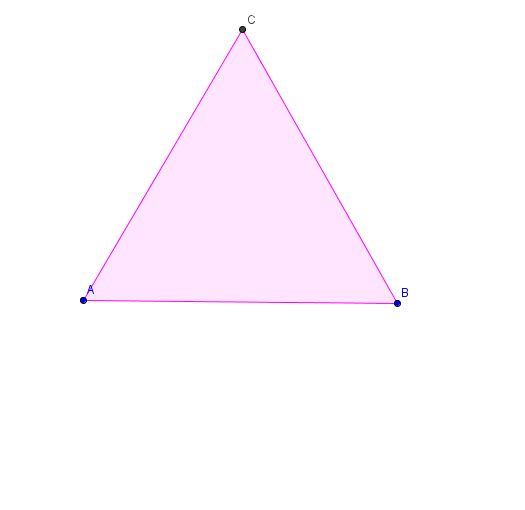
   Jak mogłeś zaobserwować niezależnie od kształtu trójkątów podobnych trójkąt PQR zawsze był równoboczny. A co by było gdyby ABC był równoramienny, prostokątny albo jeszcze inny? To pozostawiam już tobie, drogi czytelniku, do zbadania. Pomogę ci zacząć z trójkątem równobocznym, gdzie jeden bok jest innej długości niż pozostałe więc pokaże ci jak skonstruować trójkąt podobny na tym krótszym boku:
   1. Narysuj trójkąt równoboczny i trójkąt na jego najdłuższym ramieniu.
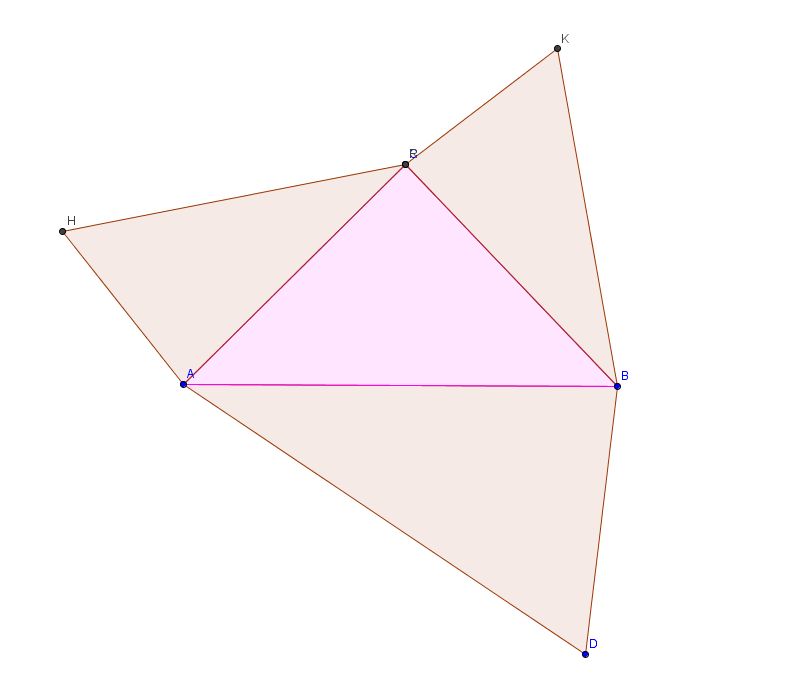
   2. Zakreśl okrąg o środku w jednym z końców odcinka przy którym zbudowaliśmy przed chwilą trójkąt a promieniu równym bokowi trójkąta, na którym teraz budujemy trójkąt.
   3. Oznacz punkt przecięcia okręgu ze wspólnym bokiem dwóch trójkatów jako F.
   4. Poprowadź prostą równoległa do jednego z dwóch boków trójkąta, którego "podobiznę" budujemy i przechodząca przez punkt F
   5. Oznacz przecięcie tej prostej z trzecim bokiem trójkąta jako G.
   6. Trójkąt powstały z dwóch boków "starego" trójkąta i prostej jest już naszym trójkątem. Teraz wystarczy przenieść tylko długości boków i gotowe.
   Jeżeli jednak jesteś wzrokowcem albo coś nie do końca zrozumiałeś oto jak ten proces powinien przebiegać:.
   Teraz spróbuj stwierdzić kiedy PQR jest równobocznym w zależności od trójkąta ABC i trójkątów podobnych. Powodzenia.
   Przedtem trójkąty wybudowane na bokach były równoboczne więc zamiast 4 punktów szczególnych (ortocentrum, środek ciężkości, środki okręgów opisanego i wpisanego) miały tylko jeden punkt S. Poszukując odpowiednika twierdzenia Napoleona dla trójkątów podobnych zamiast równobocznych warto sprawdzić czy między trójkątami powstałymi z połączenia odpowiednich środków nie ma jakiś korelacji i czy te trójkąty nie mają jakiś specjalnych własności.
   Tak więc sprawdźmy wzajemne położenie tych trójkątów: (Orto - ortocentra, SC - środki ciężkości, O - środki okręgów opisanych, o - środki okręgów wpisanych)
   (Jeżeli chciałbyś dokładneij zbadać omawiany teraz problem sama kartka papieru może nie wystarczyć, dlatego polecam spróbowanie konstruuowania w jednym z programów geometrycznych takich jak Geogebra. Możesz także zdać się na moje konstrukcje ufając że nie popełniłem żadnego błędu:)
   i ich zmiany przy zmianach trójkatów podobnych:
   Ja niestety nic specyficznego nie zauważyłem. A ty? Tak więc raczej nie istnieje coś takiego jak odpowiednik twierdzenia Napoleona dla trójkątów podobnych. A co z pokrywaniem się środków ciężkości? Sprawdźmy je dla wszystkich czterech trójkątów: (gdzie X to środek cięzkości ABC, a S1, S2, S3 i S4 to odpowiednio środki ciężkości trójkątów utworzonych przez te same punkty z różnych trójkątów)
   Jak mogłeś zauważyć wszystkie środki cięzkości się pokrywają. Zaskakujące? Sprawdź więc nastepującą rzecz i powiedz czy cię zaskoczyła: "Wybierz w jednym z trójkątów podobnych taki punkt M że od wierzchołków trójkata będzie odległy o odpowiednio a, b i c. W drugim trójkącie podobnym wybierz taki punkt N aby od wierzchołków tego trójkąta był odległy o d, e i f oraz żeby a/d=b/e=c/f= stopniowi wzajemnego podobieństwa trójkątów. Analogicznie w trzecim trójkącie podobnym wybierz punkt O (prościej niestety nie umiałem wytłumaczyć ale na rysunku napewno od razu zrozumiesz o co chodzi). Czy środek ciężkości trójkata MNO i ABC pokryją się?"Odpowieź brzmi: tak.
   Po przeczytaniu uwaznie całej mojej pracy powinnieneś umieć udowdnić przedstawioną tutaj zależność, jeśli jednak nie masz ochoty zagłębić się bardziej w tajemnice matematyki - twoja strata. Tym jednak, których trochę zaciekaiłem poruszanymi tu problemami, mogę dać mało podpowiedź: Podaną sytuację da się łatwo sprowadzić do sytuacji, gdy M N O są wierzchołkami trójkątów podobnych:
   Niezależnie czy tylko ogladałeś animacje czy uwaznie czytałeś każde zdanie i samemu próbowałeś coś konstruować, mam nadzieję że moja praca ci się spodobała i zaciekawiła cię goemetrią, konsrtukcjami w programach takich jak Geogebra, czy sposobami wykorzystania kartki i ołówka. 
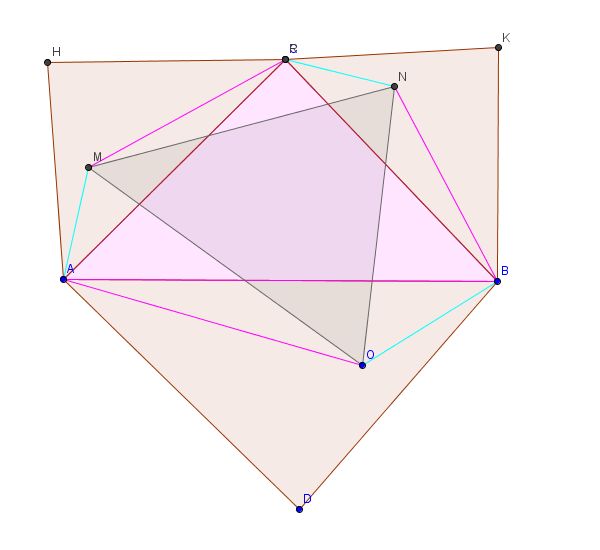
   Dziekuję za uwagę.

Autor:
Aleksander Konior
 uczeń LO nr 1 im. Stanisława Konarskiego w Oświęcimiu

Bibliografia:
-Witold Pająk "Analiza problemów otawrtych wspomaganych Cabri" DLA SZKOŁY Wilkowice1999
-Bronisław Pabich "Odkrywanie geometrii trójkąta z Cabrii 1.7 i Cabri II" Biblioteczka Cabristy nr 2
-moje notatki (jeszcze nie wydano)