Wspólny wierzchołek ścian bocznych ostrosłupa nazywamy wierzchołkiem ostrosłupa.
Rzut prostokątny wierzchołka ostrosłupa na płaszczyznę podstawy nazywamy spodkiem wysokości ostrosłupa.
Wysokością ostrosłupa nazywamy odcinek łączący wierzchołek ostrosłupa ze spodkiem wysokości ostrosłupa.
Ostrosłup nazywamy ostrosłupem prawidłowym, gdy jego podstawą jest wielokąt foremny i spodek wysokości ostrosłupa jest środkiem okręgu opisanego na podstawie.
Jeżeli ostrosłup jest
prawidłowy, to wszystkie jego krawędzie boczne są równe, wszystkie kąty
nachylenia krawędzi bocznych do płaszczyzny podstawy mają równe miary,
wszystkie ściany boczne są przystającymi trójkątami
równoramiennymi.Przyjrzyjmy się zdjęciu piramidy obok. Ma kształt ostrosłupa prawidłowego czworokątnego (podstawą jest kwadrat), który bywa nazywany właśnie piramidą. Potwierdza to tylko fakt, że z wieloma zagadnieniami matematycznymi spotykamy się w życiu codziennym.
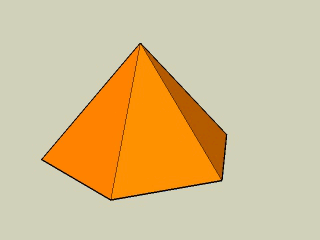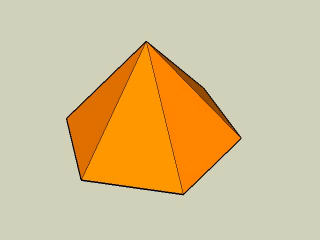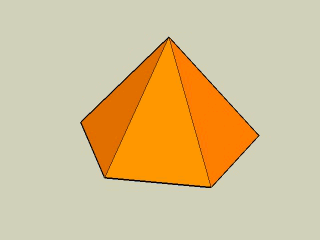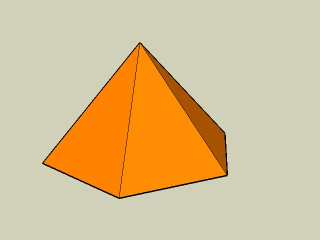
Na animacji widzimy inny przykład ostrosłupa prawidłowego - sześciokątnego. Jego podstawą jest sześciokąt foremny, a ścianami są trójkąty równoramienne. Spodek wysokości jest środkiem okręgu opisanego na podstawie.
Szczególnym przypadkiem ostrosłupa prawidłowego trójkątnego jest czworościan, którego wszystkie ściany są trójkątami równobocznymi (w każdym innym ostrosłupie prawidłowym trójkątnym to podstawa jest trójkątem równobocznym, ściany natomiast są trójkątami równoramiennymi). Czworościan należy do grupy wielościanów foremnych, więc tam też został szerzej omówiony i pokazany.
W temacie ostrosłupów warto wspomnieć jeszcze o tzw. ostrosłupach ścietych.
Ostrosłupem ściętym nazywamy część ostrosłupa zawartą między jego podstawą i przekrojem płaszczyzną równolegą do podstawy wraz z tą płaszczyzną.
Ściany boczne ostrosłupa ściętego są trapezami.
Podstawy ostrosłupa ściętego są wielokątami podobnymi.
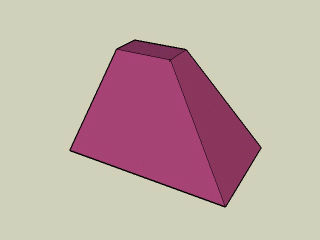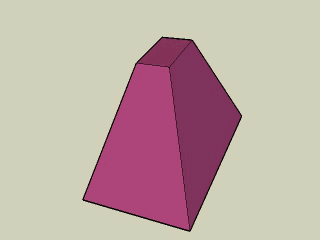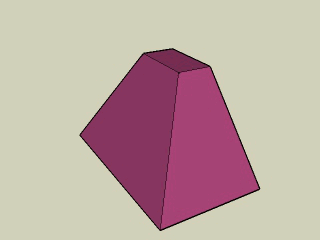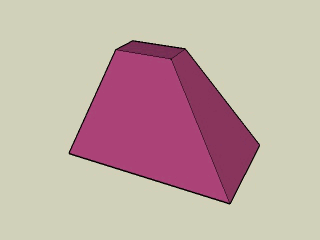
Na kolejnej animacji widzimy ścięty ostrosłup o podstawie prostokątnej. Jego górna podstawa jest podobna do dolnej. Ściany rzeczywiście są trapezami. Gdybyśmy przedłużyli krawędzie boczne tego ostrosłupa ściętego, zbiegłyby się w jednym punkcie.
Created by Anita Ciosek 2011