
Istnieje tylko pięć wieloscianów foremnych:
Czworościan (tetraedr)
4 ściany trójkątne, 4 wierzchołki, 6 krawędzi

Animacja pokazuje nam czworościan foremny.
Każda z jego ścian jest trójkątem równobocznym. Jest on szczególnym przypadkiem ostrosłupa prawidłowego trójkątnego.
Sześcian (heksaedr)
6 ścian kwadratowych, 8 wierzchołków, 12 krawędzi.

Sześcian foremny to wieloscian foremny o sześciu ścianach w kształcie identycznych kwadratów. Kąt między ścianami sześcianu jest kątem prostym. Sześcian foremny jest szczególnym przypadkiem graniastosłupa prawidłowego, prostopadłościanu i romboedru.
Na animacji możemy obejrzeć czworościan z różnych stron.

Formy sześcienne występują także w środowisku naturalnym, tak krystalizuje się np. piryt (widzimy go na fotografii obok).
Ośmiościan (oktaedr)
8 ścian trójkątnych, 6 wierzchołków, 12 krawędzi

Ośmiościan foremny to wielościan foremny o ośmiu ścianach w kształcie identycznych trójkątów równobocznych. Ma cztery pary ścian do siebie równoległych. Jest także antygraniastosłupem.
Na animacji obok ośmiościan foremny.
Dwunastościan (dodekaedr)
12 ścian pięciokątnych, 20 wierzchołków, 30 krawędzi
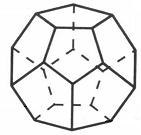
Na obrazku kolejny z wielościanów foremnych - dwunastościan. Każda z jego ścian jest pięciokątem foremnym.
Dwudziestościan (ikosaedr)
20 ścian trójkątnych, 12 wierzchołków, 30 krawędzi
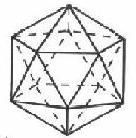
Na obrazku ostatni już z wielościanów foremnych, a już trzeci z nich, którego ściany są trójkątami równobocznymi. Ten jest jednak najbardziej z nich złożony, bo ma aż 20 ścian.
Dlaczego wielościanów foremnych nie może być więcej niż pięć?
Suma wszystkich kątów płaskich kąta bryłowego musi być mniejsza od 360°.
Z trójkątów można zbudować trzy wielościany foremne, gdzie z jednego wierzchołka mogą wychodzić:
- 3 krawędzie (60° × 3 = 180° < 360°)
- 4 krawędzie (60° × 4 = 240° < 360°)
- 5 krawędzi (60° × 5 = 300° < 360°).
Z kwadratów składać się może tylko jeden wielościan (3 × 90° = 270°).
Z pięciokątów foremnych składać się może również tylko jeden, gdyż kąt pięciokąta foremnego ma miarę 108° (3 × 108° < 360°).
Z sześciokątów, ani tym bardziej z wielokątów o większej liczbie boków, wielościanu foremnego zbudować się nie da.

Platon (427 p.n.e.-347 p.n.e.) - grecki filozof. Jako pierwszy odnotował fakt istnienia ściśle określonej liczby wielościanów foremnych. Do jego czasów znane były tylko cztery z nich (nie znano dwunastościanu - został on odkryty przez Teajtetosa, ucznia Platona) . Platon przyporządkował każdej z doskonałych brył jeden z żywiołów: ogień - czworościan, ziemia - sześcian, powietrze - ośmiościan, woda - dwudziestościan. Po odkryciu dwunastościanu foremnego włączył go do swojego systemu jako symbol wszechświata.

Johannes Kepler(1571-1630) - niemiecki matematyk, astronom i astrolog. Użył wieloscianów foremnych do swojego modelu kosmologicznego. Jeśli bowiem na sferze o promieniu orbity Merkurego opisać ośmiościan, a na nim następną sferę to jej promień będzie odpowiadać promieniowi Wenus. Jeśli na tej drugiej sferze opisać dwudziestościan, a na nim trzecią sferę to jej promień odpowiada promieniowi orbity Ziemi. I tak kolejno dla następnych wieloscianów foremnych i planet: dwunastościan - Mars, czworościan - Jowisz, sześcian - Saturn. Było to pierwsze z odkrytych przez Keplera praw ruchu planet, nie uznane jednak za prawo natury w dzisiejszym rozumieniu nauki.
Created by Anita Ciosek 2011