Składanie kwadratu lub trójkąta równobocznego

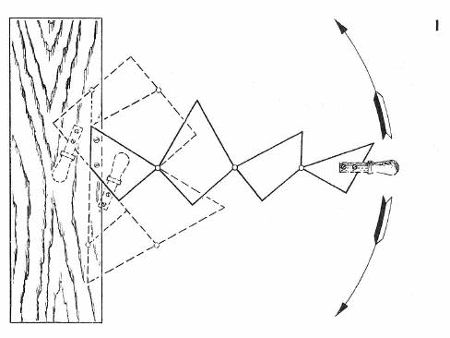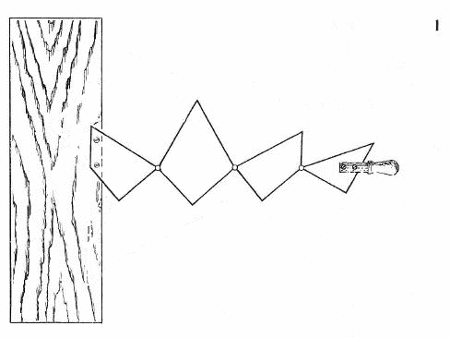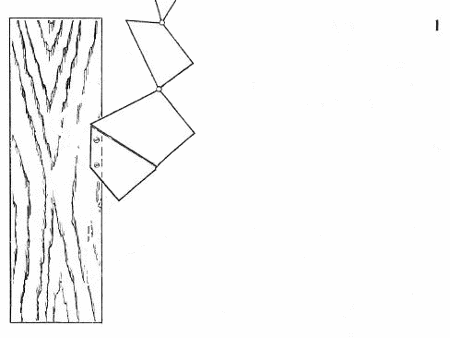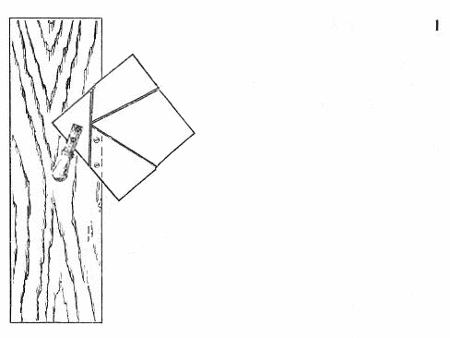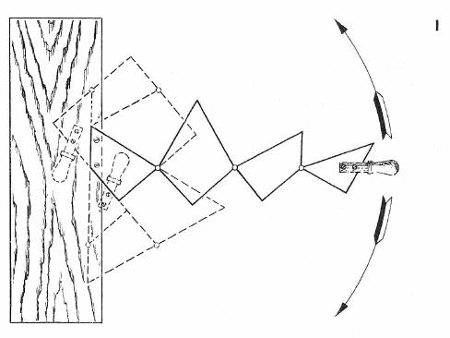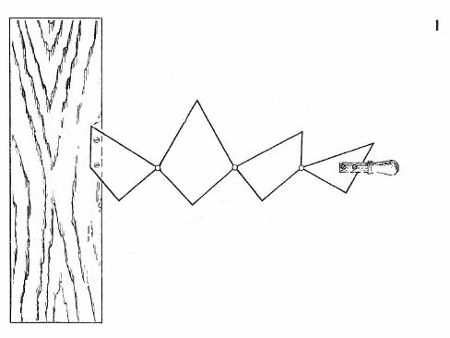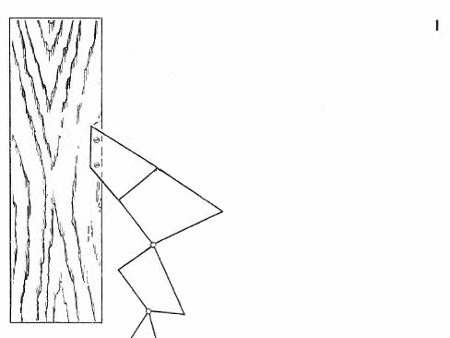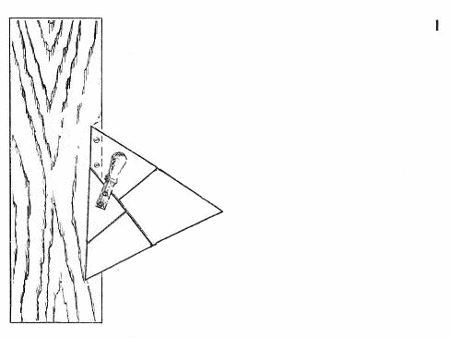Kręcąc w lewo układa nam się kwadrat a w prawo trójkąt. Oczywiście nie z każdych desek wyjdzie nam taka sytuacja. Aby wykonać coś takiego napierw musisz pociąć w podoby sposób twój trójkąt bądź kwadrat a efekt będzie taki sam. (2) gdzie kąt alfa wybrano tak, aby odcinek AB był dwukrotnie dłuższy od odcinka CD.

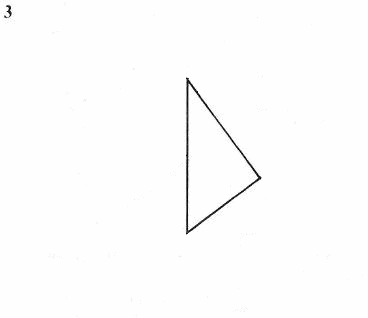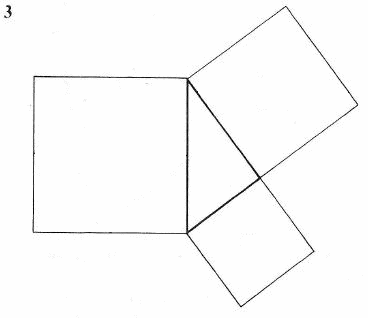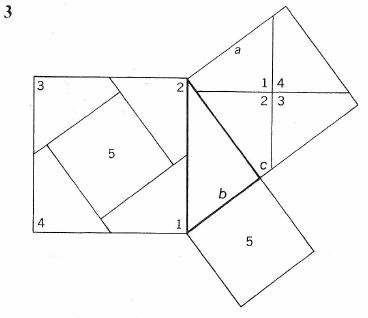
Chcąc rozłożyć kwadrat na dwa kwadraty rysujemy (3) trójkąt prostokątny, by się przekonać, że duży kwadrat jest sumą mniejszych, rozcinamy średni kwadrat na cztery części linią pionową i poziomą przez środek i przesuwamy te ćwiartki bez obracania w rogi dużego kwadratu; pozostanie w nim wola część środkowa, którą pokryjemy przesuwając na nią mały kwadrat. Że mały kwadrat akurat pasuje do wolnej części, widać z równości a = b + c.

Sens twierdzenia wyjaśnia (4) trójkąt o bokach 3,4,5 czyli 9 + 16 = 25

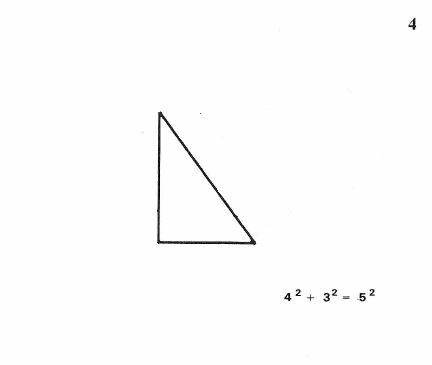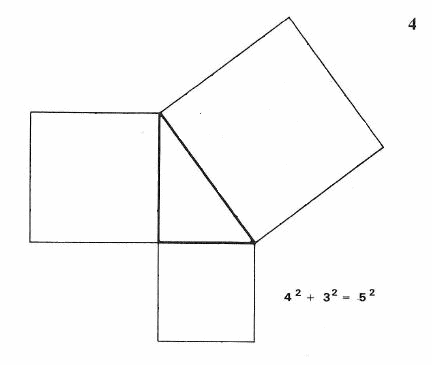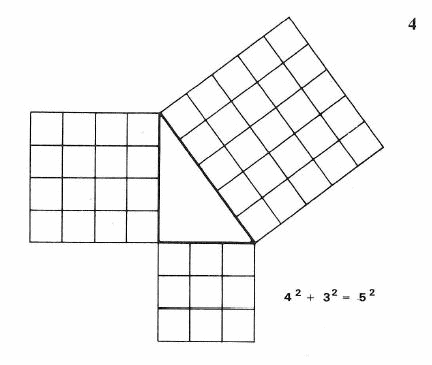
Możemy zatem narysować kąt prosty, jeżeli mamy zamknięty sznurek 12-centymetrowy, a na nim znaczki w odległości 3,4 i 5 centymetrów jeden od drugiego. Ale (5) tę samą własność trójkąta prostokątnego możemy sprawdzić bez kwadratów.

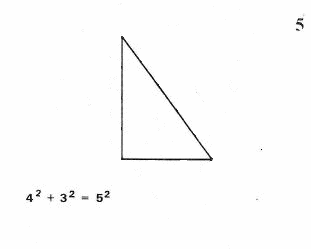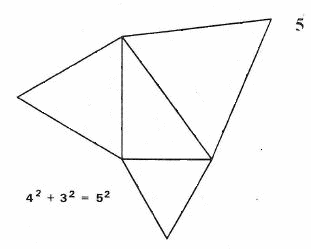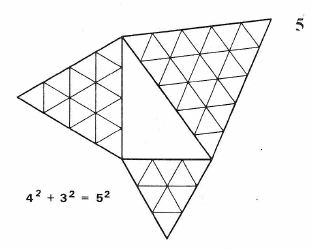
Narysujemy trójkąty równoboczne na bokach danego trójkąta ABC, którego jeden z kątów (C) ma 60 stopni (6).

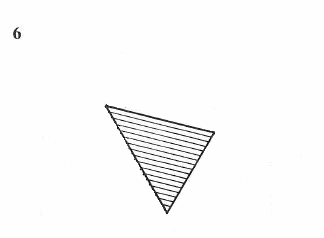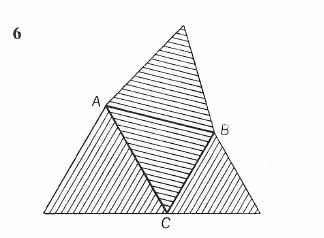
Łączne pole trójkąta ABC i trójkąta dorysowanego naprzeciw wierzchołka C jest równe sumie pól dwu pozostałych trójkątów. Wynika to z (7): 1 + 2 + 3 = 1’ + 2’ + 3’.

Chcąc otrzymać trójkąt równoboczny możemy zacząć od dowolnego trójkąta (8) i podzielić każdy jego kąt na trzy równe kąty, powstanie wtedy w środku mały trójkąt równoboczny.

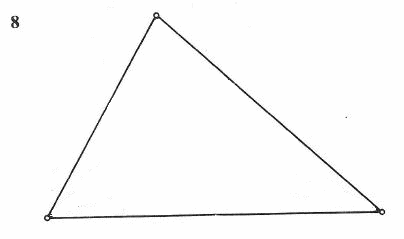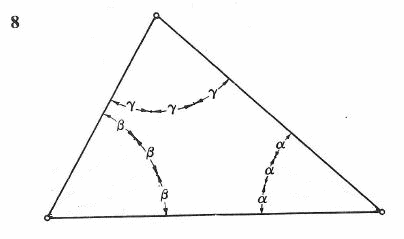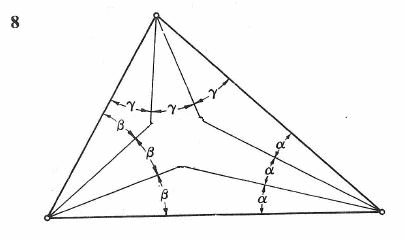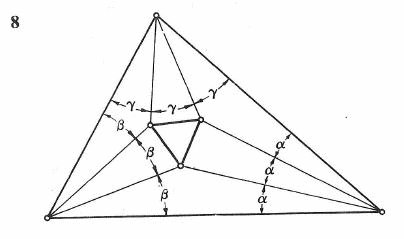
Podzielić kąt na równe kąty można bardzo dokładnie (9) dzieli się go na połowy, a potem cięciwę polówki na trzy równe części, a promień odcinający 2/3 cięciwy odcina jedną trzecią całego kąta.

Ta konstrukcja nie jest idealnie poprawna ale wystarczająco dobra.