Witaj!
Przygotowałem dla Ciebie stronę o...
Twierdzeniu Trysekcji Morley'a
Część I - Wprowadzenie
Ta linia będzie prowadzić
Cię poprzez kolejne strony!
Wzdłuż lini możesz poruszać się przesuwając pasek przewijania, bądź za pomocą
kręcenia kółkiem myszy.
Aby ułatwić eksplorację, w każdej chwili możesz przemieszczać się do wybranej przez Ciebie strony za pomocą poniższego Menu!
Część II - Treść właściwa
Słowem wstępu...
"Morley i jego cuda" - dlaczego właśnie taka nazwa pracy? Otóz Twierdzenie Trysekcji Morley'a , zwane jest też Cudem Morley'a (z ang. Morley Miracle). Wiele osób zastanawiać się może w tym momencie, dlaczego akurat to twierdzenie zasługuje na miano cudu? No i pewnie czym w ogóle jest Trysekcja? Do wszystkiego dojdziemy, ale po kolei. Póki co zapraszam do przeanalizowania mojej pracy. Chętnych namawiam również do wykonywania wszelkich rysunków na kartce, bądź nawet w programach do tego stworzonych (Geogebra, C.a.R).
Warto spróbować i nauczyć się czegoś więcej!
Frank Morley, kim był, co robił?
Angielski matematyk, zajmujący się głównie dziedzinami algebry oraz geometrii - tak właśnie można powiedzieć o Morley'u. Przez rok był przewodniczącym Amerykańskiego Towarzystwa Matematycznego. Jako ciekawostkę uznać można, iż był bardzo dobrym szachistą, pokonał nawet mistrza świata w tej dziedzinie, Emanuela Laskera. Jak wiadomo szachy wymagają analitycznego umysłu. Ale przejdźmy do interesesującego nas tematu. Jego głównym dokonaniem było odkrycie twierdzenia trysekcji w geometrii euklidesowej.
Treść Twierdzenia Morley'a
W dowolnym trójkącie, trzy punkty powstałe w wyniku przecięcia się prostych bądź półprostych dzielących
kąty trójkąta na trzy równe części, tworzą trójkąt równoboczny.
Aby troszkę rozjaśnić sytuację spójrz na animację po lewej... Ukazuje ona trójkąt równoboczny utworzony w sytuacji przedstawionej w twierdzeniu.
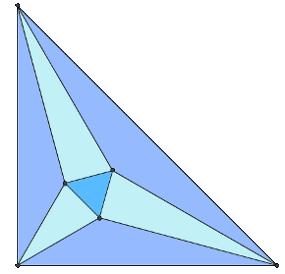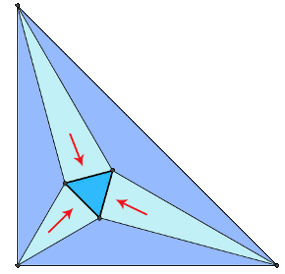Ale zanim zajmiemy się stricte tym zagadniem, dowiedzmy się najpierw czym jest Trysekcja Kąta i jak się za nią zabrać. Zapraszam dalej!
Trysekcja dowolnego kąta
↓
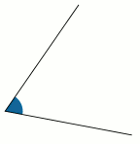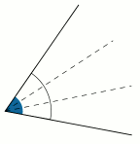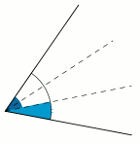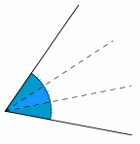
Trysekcja kąta polega na podziale go na trzy równe części. Zostało to przedstawione na animacji obok. Nie jest to jednak takie łatwe. Problem sięga swą historią do Pitagorejczyków. Już w starożytności szukano sposobu na konstrukcję dziewięciokąta foremnego. Aby tego dokonać trzeba podzielić kąt 120˚ na trzy równe części (przy użyciu podstawowych narzędzi takich jakich linijka i cyrkiel). Przysparzało to jednak niepokonane trudności.
Możesz pomyśleć: "Jak to? Przecież to proste. Sam umiem konstrukcyjnie podzielić na trzy części niektóre kąty!". Owszem istnieją pewne wyjątki
Aby przybliżyć temat muszę posłużyć się odkryciem niejakiego Pierre'a Wantzela. W 1837 roku udowodnił on, że konstrukcja trysekcyjna
dla dowolnego kąta jest niemożliwa. Dowiódł, że dla danego kąta
, kąt o mierze 1/3
jest konstruowalny wtedy i tylko wtedy gdy
wielomian
jest rozkładany w ciele
. Zanim użyjemy tego twierdzenia wyjaśnijmy je choć trochę. Przypiszemy kąt beta :
, następnie użyjemy wzoru na cosinus potrojonego kąta:
.
Pozostaje tylko przerzucić wszystko na prawą stronę i stwierdzamy, że nasz x w twierdzeniu, to nic innego jak
.
Ciało natomiast informuje nas, że pierwiastki wielomianu należą do zbioru liczb wymiernych, powiększonych o wartość cosinusa danego kąta. Teraz możemy przejść do części praktycznej. Rozważymy twierdzenie dla dwóch łatwych kątów.
A1.
Dla
Cosinus kąta 90˚ = 0. Zatem po podstawieniu otrzymamy poniższe działanie, w którym szukamy miejsc zerowych:
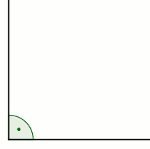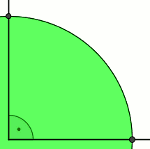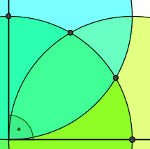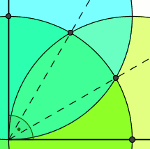
Pierwsze i trzecie miejsce zerowe jest sprzeczne, gdyż nie może przyjąć takiej samej wartości jak cosinus kąta 3 razy większego, i również cosinus przyjmuje wartości od 0 do 1, ponieważ znajduje się w pierwszej ćwiartce układu współrzędnych.
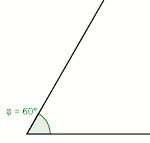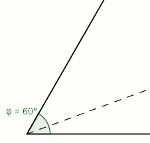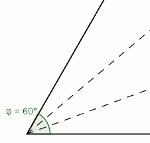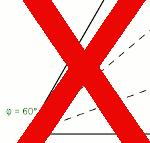
Zatem zgadza się z miejscem zerowym. Trysekcja jest konstruowalna! (sposób na obrazku, najedź kursorem aby rozjaśnić!)
A2.
Dla
Cosinus tego kąta wynosi 1/2. Zatem równanie przyjmie postać:
Szukamy pierwiastków zgodnych z ciałem, czyli w tym wypadku jedynie wśród liczb wymiernych
(gdyż
)
Wynika z tego iż jedynymi miejscami zerowymi mogłyby być liczby -1 lub 1. Niestety żadna z nich nie spełnia równania!
Konstrukcyjna trysekcyjna (za pomocą prostych narzędzi) kąta 60˚ nie jest możliwa!
Wiemy już co nieco o trysekcji. Najwiązując jeszcze do niej, chcę zauważyć, że konstrukcyjnie da się dzielić np. kąty
które są wielokrotnościami 9. Wantzel nie mylił się, mówiąc że trysekcja za pomocą prostych narzędzi jest niemożliwa, gdyż kątów które nie da się dzielić jest nieskończenie wiele.
Ponadto jeśli weźmiemy dowolny kąt (nie znamy jego miary) to konstrukcja taka jest niewykonalna za pomocą linijki oraz cyrkla.
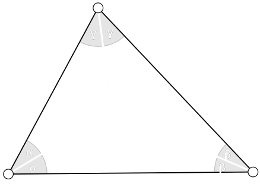Wreszcie możemy zabrać się za temat przewodni, tytułowy. Zaczerpnijmy trochę historii. Euklides w swych
"Elementach", dokładniej w Księdze IV, Twierdzeniu 4 wpisuje koło w trójkąt. Aby tego dokonać (jest to elementarna wiedza), należy
w miejscu przecięcia dwusiecznych, zaznaczyć środek wpisywanego koła. Dalej Euklides zauważył (z twierdzenia cosinusów), że długości
boków naprzeciw danych kątów są proporcjonalne do sinusów tych kątów. Ilustruje to obrazek po lewej.
Jeśli dwusieczne spotykają się w jednym punkcie to naturalne powinno być zbadanie co dzieje się w przypadku trzysiecznych. Niestety przez ponad 2000 lat, nikt się tym nie interesował (być może dlatego, iż jak pisałem na poprzedniej stronie problem stanowiło podzielenie kąta na trzy równe części).
Nikt, do czasu gdy zajął się tym Frank Morley. Odkrył, że linie dzielące kąty w trójkącie na trzy części, spotykają się w miejscach wierzchołków trójkąta równobocznego. Tyczy się to dowolonego trójkąta. Czy byłby to trójkąt rozwartokątny, czy prostokątny, czy ostrokątny, o dowolnych długościach boków - twierdzenie jest zawsze prawdziwe.
Spójrz teraz na figurę obok. Możesz złapać kursorem za wierzchołki tego trójkąta i dowolnie je przesuwać (po zadanej płaszczyźnie). Jak widzisz niezależnie od pozycji wierzchołków, czy wyglądu trójkąta, w miejscu przecięcia trzysiecznych znajdują się wierzchółki trójkąta o trzech bokach takiej samej długości. Istnieje kilka dowodów na potwierdzenie poprawności twierdzenia. Jedne mniej, inne bardziej bezpośrednie. Ja postanowiłem przedstawić dwa z nich. Twierdzenie Trysekcji Morley'a ma też różne uogólnienia, ale o tym może potem. Póki co zajmijmy się dowodami...
Pierwszym z dowodów który chcę przedstawić będzie dowód M.T Naraniengara.
W tym przypadku będziemy opierać się o pewien lemat.
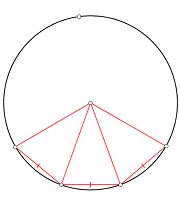Mianowicie jeśli punkty Y', Z, Y, Z' spełniają założenia:
Y'Z = ZY = YZ' oraz YZY' = Z'YZ = 180° - 2a > 60° wówczas leżą one na okręgu. Ponadto jeśli punkt A, tworzy z punktami Y' i Z' kąt
, oraz leży po stronie odcinka Y'Z' przeciwnej od punków Y, Z
to wówczas punkt A jest kolejnym punktem należącym do tego okręgu.
Na obrazku możemy zaobserwować dużo przydatnych właściwości. Czerwone trójkąty są równoramienne, gdyż ich ramiona to promienie okręgu. Łatwo zatem można określić ich pozostałe kąty.
Przejdźmy do dowodzenia twierdzenia (obrazek na białym tle).
Mianowicie jeśli punkty Y', Z, Y, Z' spełniają założenia:
Y'Z = ZY = YZ' oraz YZY' = Z'YZ = 180° - 2a > 60° wówczas leżą one na okręgu. Ponadto jeśli punkt A, tworzy z punktami Y' i Z' kąt
, oraz leży po stronie odcinka Y'Z' przeciwnej od punków Y, Z
to wówczas punkt A jest kolejnym punktem należącym do tego okręgu.
Na obrazku możemy zaobserwować dużo przydatnych właściwości. Czerwone trójkąty są równoramienne, gdyż ich ramiona to promienie okręgu. Łatwo zatem można określić ich pozostałe kąty.
Przejdźmy do dowodzenia twierdzenia (obrazek na białym tle).
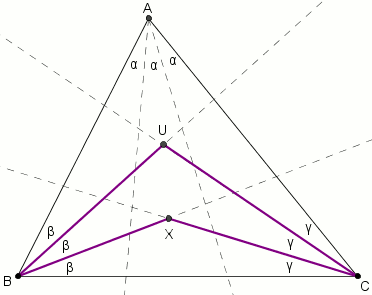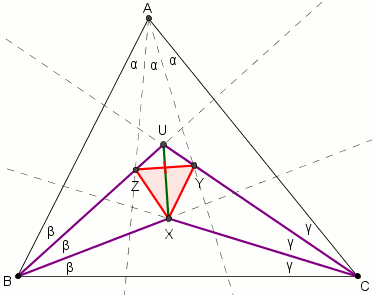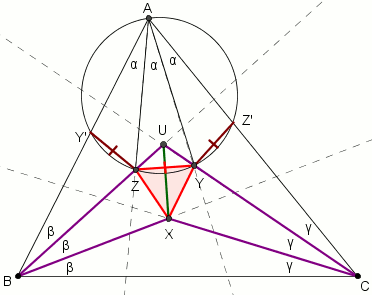
- Rysujemy dowolny trójkąt i trzysieczne kątów w nim zawartych.
- Trzysieczne kątów przy wierzchołkach B i C spotykają się w punktach U i X. W trójkącie BCU, BX i CX to dwusieczne kątów przy podstawie. Wynika z tego iż X jest środkiem trójkąta i odcinek UX jest dwusieczną kąta przy U.
- Konstruujemy punkty Y oraz Z na BU oraz CU takie, że kąt ZXU = YXU = 30°. W takiej sytuacji trójkąty ZXU i YXU są przystające (kąt-bok-kąt) - zatem XY = XZ i trójkąt XYZ jest równoboczny.
- Zauważamy również iż trójkąt UZY jest równoramienny, a jego kąty przy podstawie wynoszą
(bo kąt przy wierzchołku U wynosi 
)
Wykorzystamy też zależność 
- Kolejny krok to konstrukcja punktów Y' na AB oraz Z' na AC takich by BY' = BX oraz CZ' = CX. Wówczas trójkąty BZX i BZY' są przystające (bok-kąt-bok), tak samo ma się to trójkątów CYX oraz CYZ'.
- Przytaczamy lemat. Sprawdzamy założenia. Pierwsze z nich się zgadza. Wyliczmy drugie (podstawiamy dane). Okazuje się że
co jest zgodne z drugim założeniem. - Analogicznie postępujemy w przypadku kąta Z'YZ. Z lematu wynika, że skonstruowane przez nas punkty X,Y,Z są w istocie miejscami przecięć trzysiecznych kątów w trójkącie ABC. Q.E.D
Drugi dowód polega na dowodzeniu odwrotnym. Zatem pierwszą figurą jaką narysujemy będzie trójkąt równoboczny.
A dowodzić będziemy, że dla takiego trójkąta można zbudować dowolny trójkąt którego trzysieczne przetną się w wierzchołkach danego trójkąta równobocznego.
Jest to dowód D.J. Newmana. W poprzednim dowodzeniu powoływaliśmy się głównie na geometryczne własności, tutaj użyjemy trochę trygonometrii.
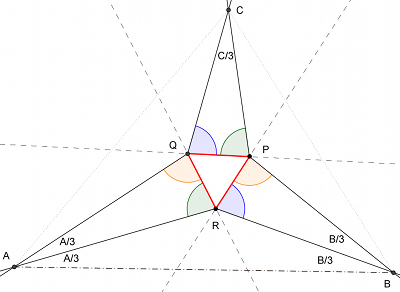
- Zaczynamy od narysowania trójkąta równobocznego i przedłużenia jego boków.
- Załóżmy że boki tego trójkąta mają długość 1. Znacznie ułatwi nam to potem obliczenia. Tak na prawdę boki mogą być dowolnej długości.
- Przy każdym z ramion trójkąta konstruujemy kąty, tak jak na obrazku. Generalnie chodzi o to by powstały pewne zależności pomiędzy tymi kątami.
Przy jednym ramieniu konstruujemy kąty takiej samej miary. Kąty przyjmują kolejno miary (zielony)
, (pomarańczowy) 
, (niebieski) 
oraz muszą spełniać zależność
. - Zauważamy, że wszystkie długości odcinków przez nas skonstruowanych są uzależnione od skonstruowanych kątów (kąt-bok-kąt).
- W trójkącie AQR stosujemy twierdzenie sinusów, które daje nam stosunek :
- Podobna sytuacja ma miejsce w trójkącie BPR, wynika z tego że :
- Obliczamy kąt ARB:
i analizujemy trójkąt ABR. - Znamy w nim kąt oraz dwa boki (własność bok-kąt-bok) zatem pozostałe kąty muszą być od tego uzależnione. Wynoszą odpowiednio A/3 oraz B/3. Co kończy nasz dowód. Aby to sprawdzić można raz jeszcze użyć twierdzenia sinusów. Q.E.D
Generalizacja Twierdzenia Morley'a
↓
Wspomniałem wcześniej, że istnieje uogólnienie tego twierdzenia. Zostało opublikowane w 1900 roku.
Również przez Morley'a. Mówi ono o sytuacji gdy weźmiemy pod uwagę również kąty poza trójkątem. Wówczas w miejscach przecieć trzysiecznych
kątów wewnętrznych i zewnętrznych powstaną kolejne cztery trójkąty równoboczne, z czego jeden z nich proporcjonalny do pierwszego poznanego w zwykłym twierdzeniu.
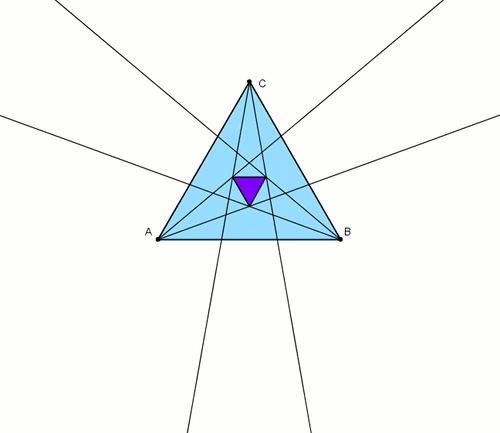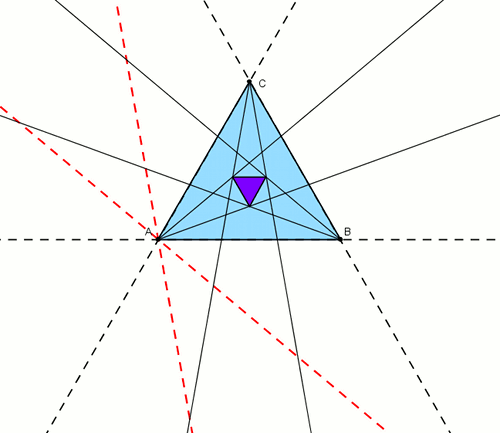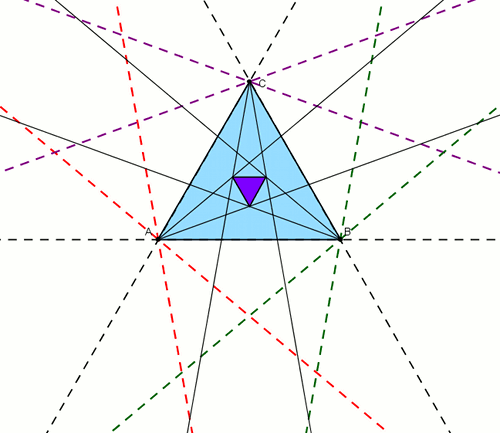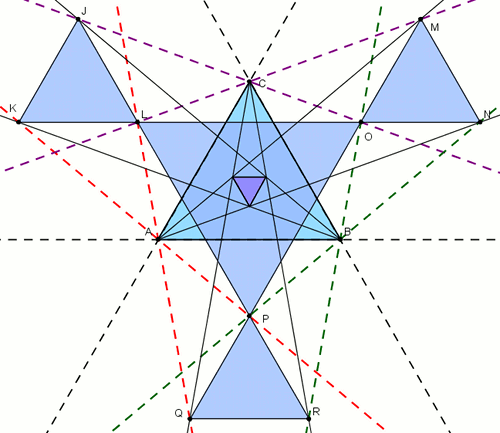
Animacja obok, krok po kroku przedstawia tę sytuację. Przeanalizujmy wszystko po kolei.- Punktem startowym jest trójkąt (dowolny) z wyrysowanymi już trzysiecznymi i postałym w wyniku tego trójkącie równobocznym.
- Należy przedłużyć każdy bok danego trójkąta.
- Następnie trzeba podzielić kąty zewnętrzne (między bokiem trójkąta, a przedłużeniem tego boku) na trzy równe części. Jak wiesz nie jest to możliwe za pomocą wyłacznie cyrkla i linijki. Ale są na to inne sposoby. Możesz wykorzystać w tym celu Konstrukcję Archimedesa. Na rysunku kolejno (czerwony) - trzysieczne kąta przy ramieniu i przedłużeniu oraz analogicznie (fioletowy), (zielony).
- W miejsach przecięcia się trzysieczych kątów, zaznaczamy punkty. Po połączeniu tych punktów, otrzymujemy interesujące nas trójkąty równoboczne. (J.K.L), (M.N.O), (P.Q.R), (L.O.P)
Część III - Pożegnanie
Gratulacje! To już koniec Twojej podróży!
Redagując treść, stawia się przede wszystkim na poprawność merytoryczną, ale nie można zapomnieć też o sposobie jej przedstawienia. Dlatego też, tworząc tę stronę miałem na uwadze przekazanie informacji w sposób atrakcyjny, przejrzysty i łatwo zrozumiały. Można z czystym sumieniem podkreślić, że gdyby nie matematyka, ta strona nigdy by nie powstała. Chodzi tutaj oczywiście o to, że przecież wszystko związane z informatyką opiera się w dużej mierze właśnie na matematyce.
Tak na prawdę codziennie "widzimy matematykę" w każdym aspekcie naszego życia!
Mam nadzieję, że moja prezentacja była dla Ciebie ciekawa, a co najważniejsze - użyteczna!
Pozdrawiam, Maciej Ziółko
"Matematyka [...] równie dobrze
może być prywatnym językiem,
zastrzeżonym dla ludzkich istot
o ludzkich mózgach, w którym coś
bazgrzemy po ścianach swojej jaskini."
~ John Maxwell Coetzee
~ John Maxwell Coetzee
- Strona została stworzona na potrzeby konkursu "Zobaczyć Matematykę".
- Wszystkie materiały użyte na stronie, zostały stworzone przeze mnie, lub są ogólnodostępne w internecie, na wolnej licencji.
- Oprogramowanie wykorzystane przy tworzeniu wszelkiego rodzaju treści jest w pełni niekomercyjne. Programy: Notepad++, GIMP, Geogebra.
- Przydatne linki wykorzystane przy opracowaniu zagadnienia (bibliografia): Wikipedia, Poncelet, Cut-The-Knot, MathPages, Konstrukcje - S. Cynk
- Techniczna część strony oparta została na skryptach Jquery, D3, ScrollPath, LaTex. Wykorzystałem również możliwości CSS3.
- Szczegółowe informacje dotyczące licencji wykorzystanych materiałów i programów znajdują się w tym pliku!
Autor: Maciej Ziółko - uczeń IV LO im K.K. Baczyńskiego w Olkuszu, klasa IIIF.