1. Liczba Phi
2. Ciąg Fibonacciego
3. Optymalne zapełnianie przestrzeni

Liczba Phi

Definicja

Złota liczba była znana już starożytnym Grekom. Jest ona ściśle związana z tak zwanym złotym podziałem. Podział ów polega na takim podzieleniu odcinka  na dwie części, aby stosunek długości dłuższego odcinka do długości krótszego odcinka był taki sam jak stosunek długości dłuższego odcinka do długości całego odcinka(|dłuższy| + krótszy|). Poniższy rysunek przedstawia graficznie powyższe zadnie.

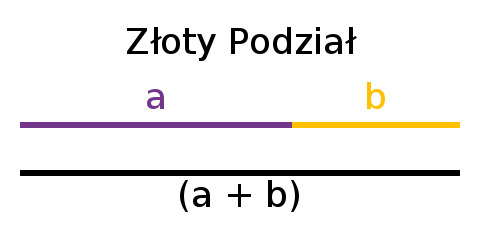
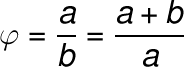
Złotą liczbę często oznacza się symbolami greckiej litery „Fi”:  Φ(fi duże) lub φ(fi małe, częściej występuje). Możemy rozwiązać powyższe równanie, i obliczyć ile faktycznie wynosi ta złota liczba.

Wzór

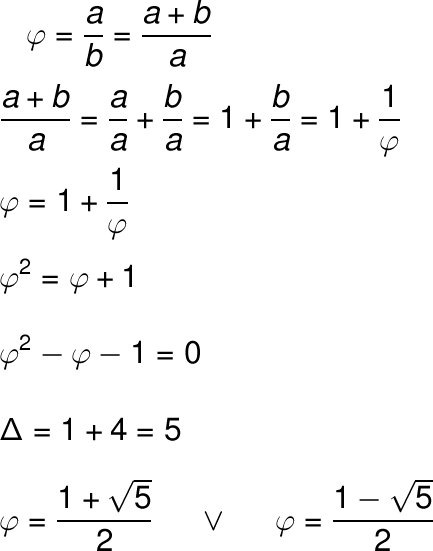
Po przeliczaniu dowiadujemy się, że Złota Liczba wynosi w przybliżeniu 1,618033988… Liczba Fi ma to do siebie, że jeżeli podniesiemy ją do kwadratu, otrzymamy liczbę dokładnie… o jeden większą. Natomiast jeżeli byśmy porównali odwrotność Złotej Liczby do jej samej, otrzymamy Złotą liczbę pomniejszoną o jeden. Drugie rozwiązanie tutaj możemy odrzucić, bo równanie tyczyło się długości odcinka, a z założenia długość taka musi być większa od zera. Mimo to warto też się nad nim zastanowić. Wynosi ono -0,618033988… Czyli tyle ile ile wynosi liczba przeciwna do odwrotności Złotej Liczby.

Całość jest bardzo ciekawa, ze względu na to, że złoty podział odcinka możemy stosować w nieskończoność, a stosunki pomiędzy odpowiednimi odcinkami będą Złotą Liczbą podniesioną do odpowiedniej potęgi.

Inspiracja

Ów liczba ma ponadto niezwykłe walory estetyczne. Starożytni architekci korzystali z niej konstruując takie budowle jak chociażby Partenon. Starali się, żeby jak najwięcej elementów względem siebie posiadało ten charakterystyczny stosunek.

Również dzisiejsi projektanci wykorzystują złotą liczbę. Poniżej widzimy wieżę "Canada's National Tower"

Znajduje ona zastosowanie ponadto w malarstwie, muzyce, czy praktycznie każdej dowolnej dziedzinie sztuki.

A wszystko to w celu... naśladowania natury(boga?) i oddawania jej piękna nawet w dziełach człowieka.

Warto zaznaczyć ponadto że same proporcje człowieka są zbliżone do złotego podziału. Sztandarowym przykładem tutaj może być stosunek wysokości osoby do długości od stóp do pępka, czy iloraz odległości między ramieniem a czubkiem palców i między łokciem a czubkiem palców.

Występowanie Złotej Liczby w budowie człowieka, jak i w naturze, jest niezwykłym zjawiskiem. Wskazuje na istnienie jakiejś wyższej reguły. Możliwych tematów do omówienia jest bardzo dużo, toteż skupię się na jednym konkretnym. Mianowicie jak Matka Natura wykorzystuje dostępną przestrzeń. Zainteresowanych tematem odsyłam do naprawdę świetnej strony gromadzącej informacje o złotej liczbie.

Ciąg Fibonacciego

Prostymi słowami: każdy jego element jest sumą dwóch poprzednich.

A gdzie tu złoty podział? To stosunek jednego elementu do elementu go poprzedzającego. Im większe wybierzemy elementy tym większą uzyskamy dokładność.

Wynika z tego bardzo ważna zależność, każdy kolejny element możemy uzyskać, mnożąc pierwotny przez złoty podział. Gdybyśmy natomiast dzielili bardziej odległe elementy, uzyskamy liczbę phi podniesioną do potęgi [ilość elementów pomiędzy]+1

W standardowej wersji Ciągu Fibonacciego elementami początkowymi są 1 i 1, w Ciągu Lucasa są to 2 i 1. Tak naprawdę mogą to też być dowolne liczby. Mówimy wtedy o Uogólnionym Ciągu Fibonacciego. Niezależnie od elementów początkowych, najważniesza własność jest zachowana. Stosunek jednego elementu do elementu go poprzedzającego, to liczba Fi.
Więcej o Uogólnionym Ciągu można poczytać stronie dr. Ron'a Knott'a

Jako że Ciąg Fibonacciego i złoty podział to bardzo sprzężone zagadnienia, warto przytoczyć kilka niesamowitych właściwości Ciągu Fibonacciego. Proszę mieć na uwadze, że ciąg, jak i każda jego odmiana, bezpośrednio wynika z liczby Phi!

Wybrane własności

Dowolny element

Możemy wyznaczyć wartość elementu ciągu Fibonacciego znając tylko jego pozycje w ciągu. Wzór dla Ciągu Fibonacciego gdy f(0) = 1 i f(1) = 1:

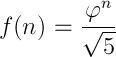
Jordan Malahi Dant wyznaczył natomiast wzór:

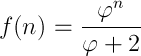
gdy f(0) = 0, f(1) = 1.
Zgromadzenie wzorów dotyczących powyższych zagadnień można zaleźć tutaj.

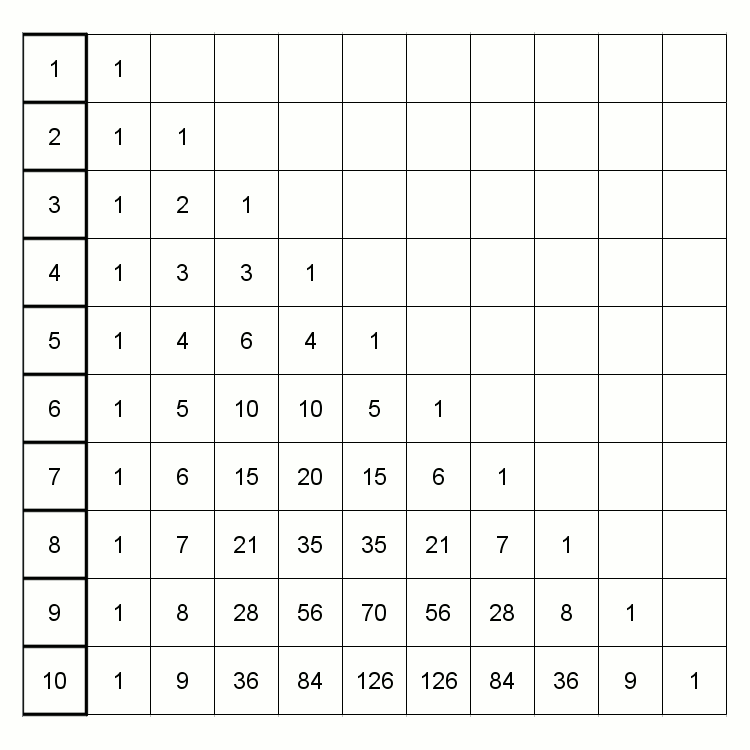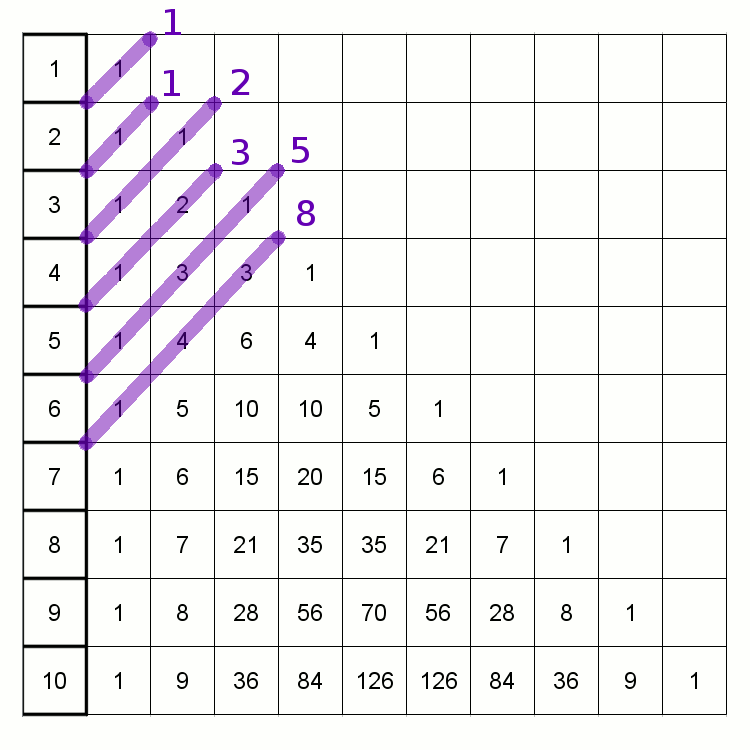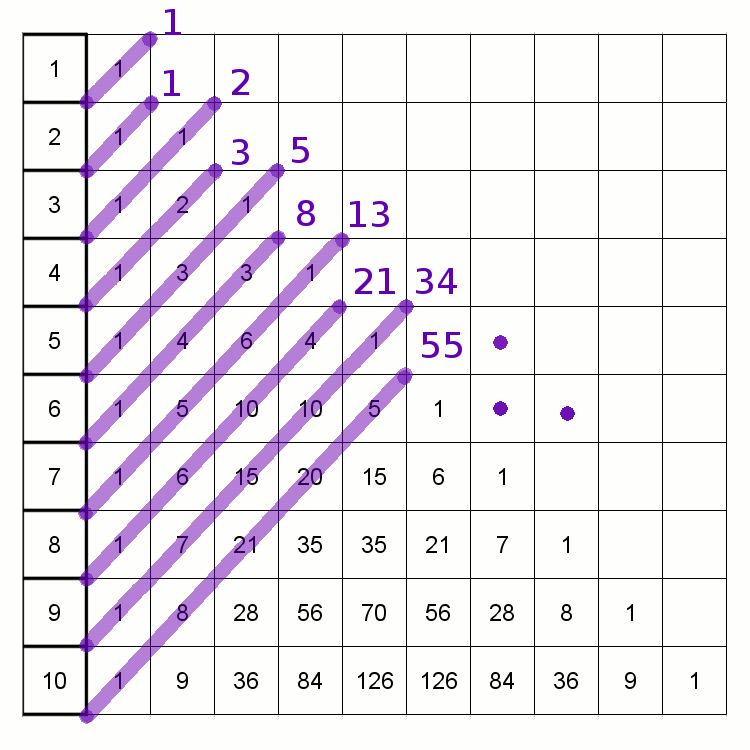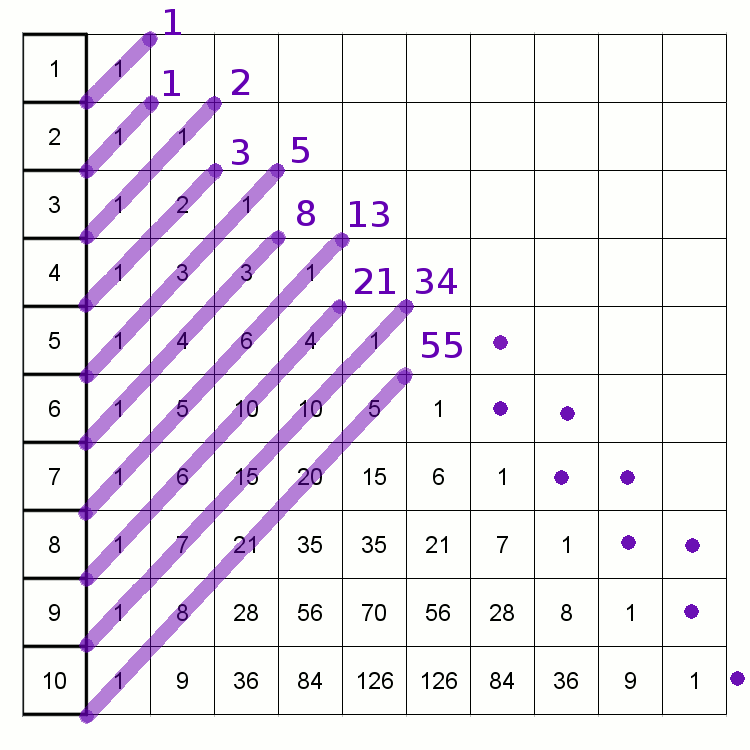
Trójkąt pascala

Posiada on oprócz bardzo wielu swoich charakterystycznych cech, związek ze Złotym Podziałem, jednakże pośrednio poprzez ciąg Fibonacciego. Poniższa animacja przedstawia tą cechę.

„Eleven Is the Sin”

...jak pisze Marvolo Livo w [1]. Jeżeli weźmiesz dowolne dziesięć kolejnych elementów (uogólnionego) ciągu Fibonacciego i je zsumujesz, to otrzymasz jedenasty element w kolejności.

Trójki Pitagorejskie

Weźmy cztery kolejne elementy z Uogólnionego Ciągu Fibonacciego i oznaczmy je literami kolejno: a, b, c oraz d. a i d nazwiemy również skrajnymi, b i c wewnętrznymi.

Wtedy prawdziwe jest zdanie: Suma kwadratów iloczynu elementów skrajnych oraz podwojonego iloczynu elementów wewnętrznych, jest równa kwadratowi sumy kwadratów elementów wewnętrznych

Można to zapisać również tak:

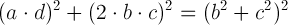
Jeżeli popatrzymy na powyższą równość przez pryzmat Twierdzenia Pitagorasa, zauważymy że wartości "w nawiasach" tworzą Trójkę Pitagorejską, czyli trzy takie liczby, z których można zbudować trójkąt prostokątny. Powyższe równanie można łatwo udowodnić, korzystając z faktu, że:

1. Wartość każdego elementu Ciągu jest równa iloczynowi jego poprzednika i Liczby Fi
2. Liczba Fi podniesiona do kwadratu daje Liczbę Fi powiększoną o jeden

Artykuł o tym można znaleźć również w książce autora Marvolo Livo [2].

Optymalne zapełnianie przestrzeni

Natura, jak to często bywa, musi borykać się z wieloma problemami. Jednym z nich jest jak najlepsze zagospodarowanie dostepną przestrzenią, na przykład w celu zdobycia odpowiedniej ilości promieni słonecznych dla liści roślin czy też, zmieszczenia jak największej ilości elementów w danym obszarze(jak chociażby pestki słonecznika).

Rozpatrzmy następującą sytuację. Istnienie układ współrzędnych biegunowych. Mogą w nim znajdować się punkty o określonym promieniu(odległości od środka, zaznaczony na czerwono) i określonemu kątowi względem 0°(zaznaczony na żółto).

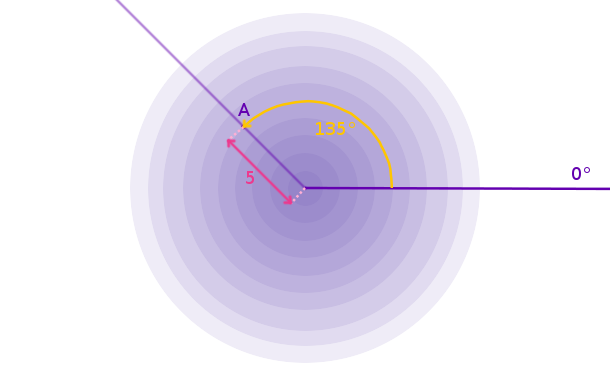
Każdy odcień to inna wartość odległości, tutaj jedna zmiana barwy na jaśniejszą to wzrot odległości o 1

Rozmieszczanie punktów na płaszczyźnie

Ilość punktów które będziemy pozycjonować oznaczymy literką N. Odległość każdego punku( R(x) )od środka wynosi √x { gdzie x to numer punktu oraz x należy do [1, N] }. Kąt każdego kolejnego punktu będzie większy o Θ (theta) od punktu o numerze o jeden mniejszym. Θ będzie współczynnikiem w naszych obliczeniach. Kąt punktu 1. wynosi zero.

W zależności od współczynnika theta punkty ułożą się w różnych prawidłowościach.

Aplikacja

Powyższa aplikacja prezentuje graficznie nasz problem. Możemy dobierać wartości poszczególnych parametrów i sprawdzać jak "wygląda" wynik.

Jeżeli Θ będzie równe 2 * Π / m , gdzie m jest różne od zera i m jest naturalne, to będziemy widzieć że punkty układają się w dokładnie m półprostych zaczynających się w środku okładu współrzędnych.
Np. dla

Zupełnie inaczej sprawa się miewa gdy za m podstawimy jakąś liczbę dowolną wymierną, lub rzeczywistą(de facto wymierną, ale przybliżoną). Widzimy że tendencja do tej prostej regularności zanika. Możemy stwierdzić, że punkty są rozłożone całkiem proporcjonalnie.(Dodatkowo polecam spróbować zmienić rozmiar obiektów)
Np:

Ale... Co jeżeli za m podstawimy Liczbę Phi ?

Jest tak jak moglibyśmy się tego spodziewać, punkty również są „równo” rozłożone. Ale porównajmy konkretnie czym rozmieszczenie punktów będzie się różnić. Przedstawia to poniższa animacja. Widzimy że mimo wszystko Phi ładniej wypełniło przestrzeń niż √3, tam gdzie jest √3 widać takie jakby „fale” emanujące od środka, tworzone przez niewielki wzrost ilości białych przestrzeni. W przypadku Liczby Phi coś takiego nie występuje, co daje powody do zastanowienia się.

Porównanie

Prawo- i lewo- skrętne spirale

Charakterystyczną rzeczą dla rozmieszczenia tych punktów dla współczynnika Fi jest ilość prawoskrętnych i lewoskrętnych spirali, a dokładniej stosunek ich ilości do siebie. Policzmy ile ich jest.

Na powyższej animacji, ich ilości oznaczone są dla prawoskrętnych na niebiesko, i jest ich 34, zaś dla lewoskrętnych na zielono i jest ich 21. 21 i 34, czy te liczby brzmią znajomo? (Równiutko z Ciągu Fibonacciego) Ich iloraz jest równy w przybliżeniu 1,619, co jest bliskie liczbie Phi(1,618033...), czyli naszemu współczynnikowi, biorąc pod uwagę że N jest względnie małe. Dla większych wartości, te liczby będą odpowiednio większe, a ich proporcja zachowana.

Ilość spiral prawoskrętnych i lewoskrętnych jest równa kolejnym elementom ciągu Fibonacciego, gdy współczynnik wynosi 2 * Π / phi.

Spirale... Złote Spirale?

Mało tego, spirale które zaznaczyliśmy nie ją pierwszymi lepszymi spiralami. Gdybyśmy je odpowiednio przedłużyli i równo pozaznaczali, ich wygląd będzie zbliżony do Złotej Spirali. Złota spirala prezentuje się następująco:

Również złotą spiralę możemy stosunkowo prosto narysować w układzie współrzędnych biegunowych. Wystarczy tylko odpowiednio modyfikować promień w miarę zwiększania kąta(i nie zatrzymywać się po 2Π.

Złotą spirale można ponadto skonstruować opierając się tylko na kolejnych elementach Ciągu Fibonacciego. Wystarczy rysować wynikające z siebie ćwierć okręgi o promieniach będącymi Liczbami Fibonacciego, co 90°.

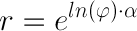
Natura

A jak to wszystko się ma do Matki Natury i jej Problemów?

Powyższy "schemat" układania elementów nie tyczy się tylko "powierzchni płaskich". Równie dobrze, może on kreować:

Szyszki z kosodrzewiny tatrzańskiej :)

Albo ananasa

Cóż, ciężko będzie pokazać jak zliczam, zostaje wam zaufanie, że ilość prawoskrętnych wynosi 13, a lewoskrętnych 8. Jeżeli ktoś chciałby zobaczyć zliczanie, polecam wideo użytkowniczki YouTube, ViHart.

Rozwój liści roślin również przebiega w ten sposób. Natura nie bez powodu wybrała złoty podział, wybrała go aby jak najoptymalniej rozwiązać swoje problemy. Człowiek dostrzegł w tym piękno i sam stara się ją naśladować.

Animacja złotych spirali

Przypisy

Andrzej Golonka, 2013, ZobaczyćMatematykę